Log-Odds in Sherwood Forest

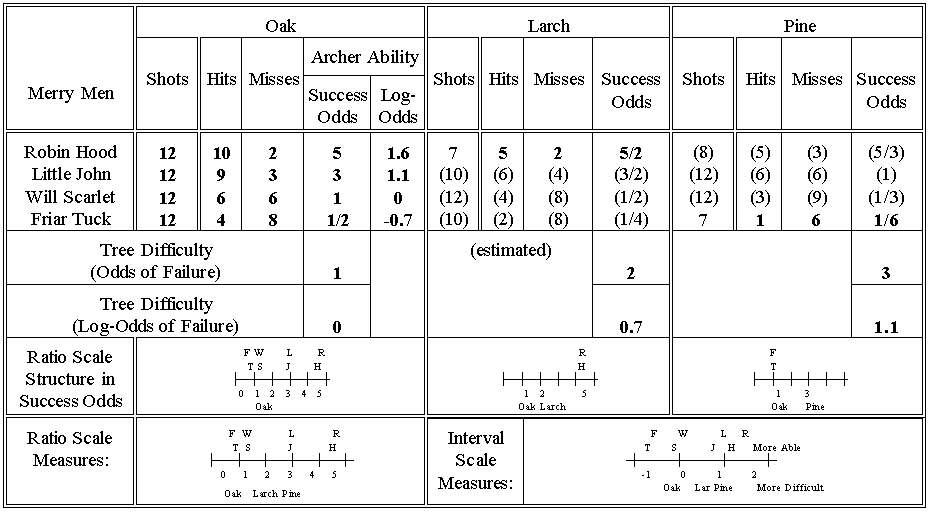
Once upon a time Robin Hood held an Archery competition. The targets were an oak, a larch and a pine. Robin Hood, Little John, Will Scarlet and Friar Tuck participated. Maid Marion kept score. First, they all shot 12 arrows at the Oak. Robin had 10 hits, John had 9, Will had 6, and Tuck had 4. Firing so many arrows took a long time, so, to speed things up, they shot at the other trees simultaneously. Robin started firing at the Larch and Tuck at the Pine. But the competition came to a sudden halt when the Sheriff of Nottingham was sighted, and everyone ran for cover. Will Scarlet asked Maid Marion for the final score. "Robin and Tuck both fired 7 more arrows. Robin hit the Larch 5 times, but Tuck only hit the Pine once". "How would I have fared on those other trees?" mused Will. Can we answer his question?

Thinking only about the Oak, we might say that Robin is 4 hits better than Will and 6 better than Tuck. Then, since Robin hit the Larch 5 times, we might expect Will to hit it 5-4 = 1 time. But then Tuck would hit it 5-6 = -1 times. This line of reasoning gives a nonsensical result because the worst Tuck could do is hit it 0 times.

Another approach could be based on proportions of success. Robin hit the oak 10 times to Will's 6 times, i.e. Will hits the oak 6/10 the times of Robin. Then, since Robin hits the Larch 5 times, we might expect Will to hit 5x(6/10) = 3 times. This sounds reasonable. But turn it around. Robin missed the Oak 12-10 = 2 times. Will missed the Oak 12-6 = 6 times. So Will misses the Oak 6/2 = 3 times more than Robin. Robin missed the Larch 7-5 = 2 times, so we might expect Will to miss it 2x3 = 6 times, and so only hit it 7-6 = 1 time. What a paradox! When we think of success, we expect Will to hit the Larch 3 times. When we think of failure, we expect Will to hit the Larch only once.

The accuracy of an archer is a combination of success and failure. At one extreme, there is all hits and no misses. At the other extreme, all misses and no hits. In the middle are half hits and half misses. 3 hits and 1 miss would seem as accurate as 6 hits and 2 misses.

Odds and Measures in Sherwood Forest

What is twice as good as 6 hits and 2 misses? Reasonable answers are 6 hits and 1 miss, or 12 hits and 2 misses. We need to combine hits and misses in such a way that 3 hits and 1 miss give the same index of accuracy as 6 hits and 2 misses, but 6 hits and 1 miss or 12 hits and 2 misses are twice as good. The only simple solution is that 3/1 = 6/2 = 3. Then a performance twice as good is 6/1 or 12/2 = 6, which is twice 3. It follows that the useful index of accuracy is hits/misses, known as the "odds of success".

Now compare Robin and Will. On the Oak, Robin's odds of success are 10 hits/2 misses = 5, as shown in the Table. On the Larch, Robin's odds of success are 5 hits/2 misses = 2.5. So Robin's odds of success were halved from 5 to 2.5, implying that the Larch is twice as difficult to hit as the Oak.

Will's odds of success on the Oak are 6 hits/6 misses = 1. If Will's odds on the Larch are also halved then his odds become 0.5. So, if Will shot 12 arrows at the Larch, we would expect 4 hits and 8 misses.

What about Will and Tuck? Tuck's odd's of success on the Oak are 4 hits/8 misses = 1/2. His odds of success on the Pine are 1 hit/6 misses = 1/6, one third of his odds of success on the Oak. So the Pine must be 3 times more difficult to hit than the Oak.

Will's odds of success on the Oak were 6 hits/6 misses = 1, twice that of Tuck. So we expect Will's odds of success on the Pine to be 2x1/6 = 1/3. If Will shot 12 arrows at the Pine, we would expect 3 hits and 9 misses.

These odds of success are useful, but they are on a ratio scale. Their arithmetic is multiplicative, not additive. Robin is 5 times as accurate as Will, and Will is 2 times as accurate as Tuck. So Robin's accuracy compared with Tuck's is not 5+2 = 7, but 5x2 = 10 times. It's usually more convenient to think with numbers we can add and subtract, i.e. interval measures. These would be the logarithms of the odds, the log-odds. Then Robin's accuracy compared with Tuck's would be log_e(5)+log_e(2) = log_e(10) in log-odds units (logits). The interval scale makes it clear that Little John is closer to Robin Hood than Friar Tuck is to Will Scarlet.

The additive Rasch model combines this information into one convenient formula:

Will's log-odds of success on the larch =
Will's log-odds of success on the Pine relative to Robin (his ability)
- Larch log-odds accuracy relative to Pine for Robin (its difficulty)

or, more generally,

The log-odds of success by an object on an agent =
the log-odds of success by the object on an agent at the origin of the scale (its ability)
- the log-odds of failure on the agent by an object at the origin of the scale (its difficulty)

Log-Odds in Sherwood Forest, J Linacre … Rasch Measurement Transactions, 1991, 5:3 p. 162-163

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt53d.htm

Website: www.rasch.org/rmt/contents.htm