Step Disordering and Rasch-Thurstone Thresholds

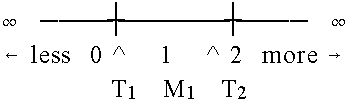
Interpreting Rasch rating scale step difficulty calibrations can be perplexing. When step difficulties increase in value, it is easy to think of the categories as ascending, if unequal, steps on a ladder. But how are step difficulties that decrease in value to be interpreted? How can a higher step on a ladder be easier to climb than one below it?

Figure 1. A rating scale on a continuum.

Figure 1 shows how a three category rating scale is used to manifest an infinite measurement continuum. 0 represents lowest performance, 1 in-between performance, and 2 highest performance. Were the empirical observations precise, then a person of ability M1 would receive all ratings in category 1. A person of ability T1, exactly at the junction of 0 and 1, would receive 50% 0's and 50% 1's, giving an expected score of exactly 0.5, and similarly for a person of ability T2, at the junction of 1 and 2.

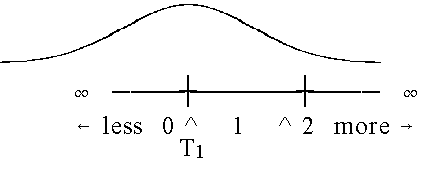Figure 2. Measures at T1 observed with error.

In practice measurement is never precise. Instead, the empirical realization of T1 has a sampling distribution like Figure 2. For a person with ability at T1, the expected ratings will be 50% 0's, 48% 1's and 2% 2's. This person's expected score will be 0.52, higher than the theoretical 0.5. But this person's median rating is still exactly between 0 and 1. T1 is the Rasch-Thurstone-type Threshold of the rating scale.

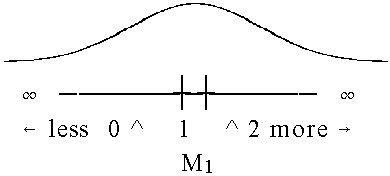Measures at M1 observed with error.

What happens when category 1 represents a narrow range of performance? Figure 3 shows an error in observing M1 such that only 30% of the observed ratings are expected to be 1's, 40% are 0's and 40% are 2's. Category 1 is not the most probable rating at M1, but it is the median rating. Step 2 from 1 to 2 is "easier" than step 1 from 0 to 1, so the step difficulty calibrations are disordered. But, now, this can be seen to present no conceptual difficulty whatsoever. The numerical step disordering is entirely a consequence of the inevitable measurement error.

Conclusion: Rasch-Thurstone-type Thresholds provide the best estimate of the transitions between categories of the rating scale. Step disorder is of no concern, provided that the structure of the scale is conceptually sound.

Step Disordering and Rasch-Thurstone-type Thresholds, J Linacre … Rasch Measurement Transactions, 1991, 5:3 p. 171

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt53k.htm

Website: www.rasch.org/rmt/contents.htm