Stress after Three Mile Island: Logistic Regression and One-facet Rasch Model

The nuclear accident at Three Mile Island in Spring 1979 produced more than radioactive fall-out. There was also publication of a Rasch analysis in a statistical journal. "[There is] a method for obtaining CMLE's [conditional maximum likelihood estimates] in the Rasch model with standard log-linear model programs such as GLIM and SPSS-X ... [This] method is used to analyze the data from the Three Mile Island study" (Conaway, 1989). What message does this paper have for Rasch measurement practitioners?

Stress in 267 mothers of young children living within 10 miles of the plant were surveyed over three years. 115 mothers, living within 5 miles of the reactor, were assigned to group LT5. The other 152 mothers, living 6 or more miles away, were assigned to group GT5. Each mother was interviewed four times, and her stress level rated high, medium or low. The data were originally published by Fienberg et al. (1985).

Conaway implemented a Rasch model in his logit-linear regression. From Table 1, one of his simpler tables, he concludes that "for the LT5 group, ... levels of stress did not change [significantly] over time". From other tables, he concludes that "in the GT5 group ... there are significant decreases in the levels of stress" (p.58). Even after reading both Conaway and Fienberg, however, I was unclear as to what had happened to mothers' stress levels. Fortunately the data matrix was also published. This afforded the opportunity to reanalyze the data with standard Rasch analysis software.

One approach is a fixed-effects, one-facet Rasch analysis (implemented with Facets). At each of time-point, each group of mothers can be thought of as random replications of a shared group/time-point stress. Since 2 groups are rated at 4 time-points, there are 8 time-point effects. Each stress rating is classified solely by group/time-point, ignoring information about which mother is rated. Thus there is just one facet containing 8 group/time-point elements. Each of the four LT5 time-point elements has 115 observations. Each of the four GT5 time-point elements has 152 observations. Since the survey is intended to have a uniform rating scale, only one rating scale structure is modelled. (An equivalent BIGSTEPS result is obtained by using a data matrix of 257 mothers by 8 group/time-points and anchoring all mothers at zero logits. Then the time-point and rating scale calibrations can be used as anchors for the analysis of time-serial effects.) The Facets output is shown in Table 2. A zero logit measure corresponds to medium stress.

The rating scale step calibrations placed the low stress region at -1.44 logits and below, and the high stress region at 1.44 logits and above. The mean-square variance ratio, "Mnsq", quantifies the extent of central tendency in the stress ratings. Values above 1.0 indicate unexpected heterogeneity in the stress ratings across mothers. Values less than 1.0 indicate unexpected homogeneity. We see that the ratings of the GT5 group are more homogeneous than those of the LT5 group.

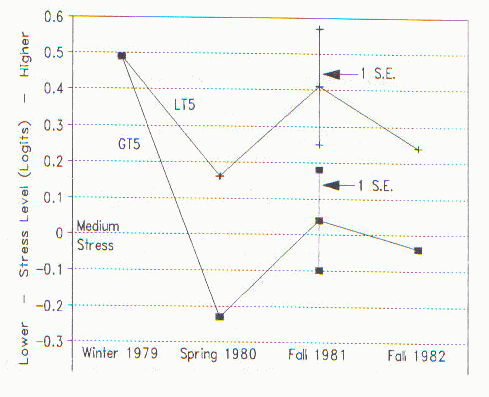
Most interesting is how stress changed over time. A plot of the 8 time-point calibrations is shown in the Figure. Immediately after the accident, the two groups of mothers were equally stressed. As time passed, the more distant GT5 group relaxed more than the LT5 group. Since each plotted point has a standard error of about 0.15 logits, the only statistically remarkable points are the first and second time points of the GT5 group. They report a significant drop in stress between Winter 1979 and Spring 1980.

What is the message? Even one-facet analysis can be useful. Though Conaway's analysis is intricate, meticulous and detailed, one simple plot can capture the whole story. John Michael Linacre

Conaway MR 1989. Analysis of repeated categorical measurements with conditional likelihood methods. Journal of the American Statistical Association, 84/5, 53-62.

Fienberg SE, Bromet EJ, Follmann D, Lambert D, May SM 1985. Longitudinal analysis of categorical epidemiological data. Environmental Health Perspectives, 63, 241-248.

   Analysis of Deviance for the LT5 Group
Model                 df   Deviance       p
----------------------------------------------
S                     45   35.94
S+H2                  44   33.58          .12
S+H2+M2               43   33.02          .76
S+H2+M2+H3+M3+H4+M4   39   30.41          .63

Table 1. Conaway's analysis of variance. S represents mothers effects. Hw and Mw stand for the medium and high stress category effects at time-point w (=2,3,4) relative to time-point 1.

Group        Total  Mean  Logit   S.E.   Mnsq.
----------------------------------------------
LT5: 115 Mothers
Winter 1979  133    1.2     .49   .16     1.2
Spring 1980  121    1.1     .16   .16     1.1
Fall   1981  130    1.1     .41   .16     1.1
Fall   1982  124    1.1     .24   .16     1.2

GT5: 152 Mothers
Winter 1979  176    1.2     .49   .14     0.8
Spring 1980  141    0.9    -.23   .14     1.2
Fall   1981  154    1.0     .04   .14     0.7
Fall   1982  150    1.0    -.04   .14     0.9

Table 2. Rasch analysis of the Stress data. Output produced by the "Facets" software.

Stress after Three Mile Island: Logistic Regression and One-facet Rasch Model. Linacre JM. … Rasch Measurement Transactions, 1992, 5:4 p.188

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt54n.htm

Website: www.rasch.org/rmt/contents.htm