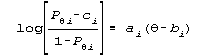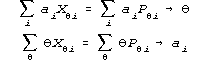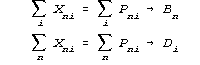IRT in the 1990s: Which Models Work Best? 3PL or Rasch?
Ben Wright's opening remarks in his invited debate with Ron
Hambleton, Session 11.05, AERA Annual Meeting 1992.
See also 3PL or Rasch?
Good morning! I was introduced as one of the debaters. I wonder
if I might not turn out to be a debunker rather than a debater. We
will find out as time goes on. As for the mysterious "one
parameter" model mentioned by Moderator, Gwyneth Boodoo, I don't
know what that is, so I can't speak for it. To my knowledge, there
are no "one parameter" models in psychometrics. There are, in fact,
only two deliberate models widely used. One is the two-parameter
Rasch Model. The two parameters (B, D) are explicit in Figure 1.
The other is the four parameter (a, b, c, θ) Birnbaum model
which sometimes has five when an upper asymptote is estimated
(Barton & Lord, 1981).
I will defend the Rasch Model. Actually, even at two parameters
(B, D) the comparison is misleading because the Rasch Model can
have any number of parameters to the right of the log-odds
statement, as long as they are connected with plus or minus signs.
As long as you maintain the additivity of measurement construction,
you can have twenty parameters off to the right, even for a
dichotomous observation. That might be a somewhat complex data
design, but we work with these things all the time these days, and
fruitfully.
Birnbaum Model: 3-PL
For 2-PL, set ci=0
For 1-PL, set ai=1.7, ci=0 | Rasch Model |
|---|
| Allan Birnbaum 1957$ / 1968 | Georg Rasch 1952$ / 1960 |
| imitates data | defines measures |
| contrived to fit observed MCQ
ICC's | derived to construct scientific
measurement |
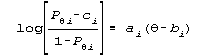
θ is the assumed, not actual, person sample distribution
|
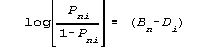
n is the actual individual person ability
|
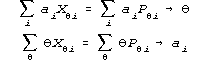
Shared ai and θ causes θ <–>
ai feedback:
divergence unless constrained |
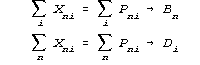
B and D estimable separately:
inevitable convergence |
MCQ dichotomies only
[1992: Eiji Muraki's Generalized Partial Credit Model] | any ordered observation
dichotomy, rating,
ranking, counting |
guessing accepted ci
reliable item
asset |
guessing rejected
unreliable person
liability |
discrimination variation
welcomed ai
as a useful item scoring weight |
discrimination variation
rejected
as a misleading item-bias interaction |
crossed ICC's accepted
natural and unavoidable
item-difficulty-ordering is different for different persons |
crossed ICC's rejected
prevents
construct validity
item-difficulty-ordering is the same for everyone |
Figure 1. Comparison of Rasch and
Birnbaum Models.
($ first written report) |
I make measures for a living. Measures have a specific
definition. They're the kind of thing where one more is always the
same amount - like inches and pounds. You may have noticed, if you
have read Thurstone (1925), Guilford (1936) or Thorndike (1904), or
thought a little, that raw scores are not measures, neither are
grade equivalents, age equivalents, percentiles or any of those
things. In science, engineering, business and cooking, you need
measures which have this simple essential property: one more is
always the same amount, like the inches on this carpenter's ruler
I am using for a pointer. To get that result, that kind of numbers,
you need to use the additive construction of the Rasch model.
It is important to clarify what these two models are about. I
will compare them to bring out how different they are. They're not
at all cases of one another. Even the arithmetical trick of making
parameters "a" and "c" disappear, so that the Birnbaum model looks
like Rasch doesn't make Birnbaum in spirit, purpose or function
equivalent to Rasch. The two are opposite in philosophy and in
practice.
The Birnbaum model is designed to imitate data, to be faithful
to the data as well as possible, to accept any kind of data,
whatever may come up. However it is contrived primarily for MCQ
response curves. Quite different from that is the Rasch model which
is not designed to fit any data, but instead is derived to define
measurement. The Rasch model is a statement, a specification, of
the requirements of measurement - the kind of statement that
appears in Edward Thorndike's work, in Thurstone's work, in
Guttman's (1950) work. Rasch is the one who made the deduction of
the necessary mathematical formulation and showed that it was both
sufficient and necessary for the construction of linear, objective
measurement. It is also nice that there are sufficient statistics
for these parameters, because that's a useful and robust device for
getting estimates. The Birnbaum model has loose standards for
incoming data. It hardly ever objects to anything because it's
adjusted to adapt to whatever strangeness there is in the data. The
Rasch model has tight standards. The two models are opposites - one
loose, the other tight - in the standards they set for the data
they will work with.
When you take a look in Figure 1 at Birnbaum's (1968) estimation
equations and compare them to the estimation equations for the
Rasch model, you notice something striking and troublesome. There's
a cross-weighting of data and parameters in Birnbaum's equations.
The discrimination estimates weight the data when you estimate
person ability, and the person ability estimates weight the data
when you estimate item discrimination. This cross-weighting
guarantees divergence. It guarantees the failure to converge
reported in almost every paper about the Birnbaum model since 1968.
In Stocking (1989), people are advised never to iterate more than
four times, because, if they do, the estimates will go further and
further away, even from the generating parameters of artificial
data made to fit the model perfectly which the model is trying and
failing to recover as it iterates.
These models are opposites. In estimation procedure they
function oppositely. The Birnbaum model is impossible to apply.
Unless you cheat, you can't apply it at all. In contrast, Rasch is
easy to apply. It takes very strange real data configurations to
prevent Rasch estimation from converging. Data configurations so
strange that, when you track them down, you discover that these
were not the data you wanted to analyze. Another polarity. Birnbaum
is hard to use. Many say impossible. Rasch is easy to use. I've
never heard of anyone being unable to use the Rasch model, whatever
ideology they may profess.
What about application? They are also opposite in application.
Because the Birnbaum model is only for multiple choice dichotomies,
that's where it stops - at a dying-out kind of item soon to be
gone. The Rasch model, in contrast, is for any kind of ordered
observation, any kind at all: a rating, a scoring, a ranking. We
have handled successfully a tremendously wide variety of data
structures. Birnbaum is narrow, about as narrow as you can get.
Rasch is wide, about as wide as you can get. So wide its limits
have not yet been encountered. There are at least nine different
formulations, kinds of models, which we can analyze with the Rasch
formulation.
Finally we come back to another aspect in which they are
opposite. It is an echo of the earlier ones. In Birnbaum we have a
kind of promiscuity. Guessing is accepted as a reliable item asset.
Discrimination is welcomed as a useful scoring weight. And crossed
item characteristic curves are accepted as natural and
unavoidable.
In Rasch, instead of promiscuity, we have choosiness. We don't
want guessing. We recognize it as an unreliable person liability.
I never met an item that guessed, so I look for guessing among
people. I do find some people who guess sometimes, but not all
people guess and seldom on the same items. So I do a better job of
identifying and controlling guessing when I look for it in persons'
responses, label it and decide what I want to do with it.
A USEFUL
RULER
WOODCOCK
READING MASTERY TESTS |
|---|
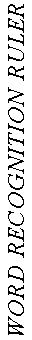 |
DIFFICULTY |
SAMPLE
TASK |
|---|
Mastery
Scale | Grade
Scale
50% Mastery |
|---|
25
41
58
70
86
101
114
124
143
159
174
192
211
240 |
 |
1.1
1.3
1.4
1.5
1.7
1.8
2.0
2.2
2.8
3.3
4.1
5.7
9.3
12.9 |
 |
is
red
down
black
away
cold
drink
shallow
through
octopus
allowable
hinderance
equestrian
heterogeneous |
A
B
C
D
E |
 |
|---|
FIXED ITEM POSITIONS
DEFINE VARIABLE |
| Figure 2. A useful, linear,
invariant measuring instrument. |
Variation in discrimination is also rejected by Rasch as a
symptom of item bias, multi-dimensionality. This phenomenon has
been followed up empirically many times (e.g., Masters, 1988). The
items which vary in discrimination have been demonstrated to be
contaminated by item bias or to introduce extra dimensions.
What I want to talk about in the minute or two I have left is
crossed ICC's. I reject them because they prevent construct
validity. Here in Figure 2 is a beautiful word-recognition ruler
constructed by another man who makes measures for a living, Dick
Woodcock (1974). In the left column are the inches on Dick's ruler.
They mean the same amount from one end to the other. In the center
column is the range of this ruler: from 1st to 12th Grade. In the
right column are the words that define this variable, that specify
its definition. "Red" is a nice short easy word. It is recognized
at the 1st Grade. But, when you get down to "heterogeneous", it
takes a 12th Grader to nail it down. We have a continuous construct
here, specified explicitly, which we can use to make sense out of
children's measures. This construct gives the scale meaning. The
identification of a stable ordering and spacing of items is
decisive for construct validity.
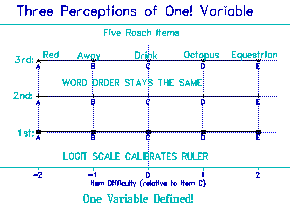
Figure 3. Five Rasch Items and Three Ability Levels
1st = Low ability; 2nd = Medium ability; 3rd = High Ability
Notice the 3 identical item-difficulty hierarchies (advancing from left to right) |
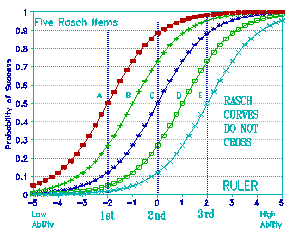
Figure 4. Five Rasch Curves and Three Ability Levels
1st = Low ability; 2nd = Medium ability; 3rd = High Ability |
Look at Figure 3. It needs to be the case that, whether you are
a 1st, 2nd or 3rd Grader, "red", "away", "drink", "octopus" and
"equestrian" remain in the same order of experienced difficulty, at
the same spacing. The ruler has to be the same for every child
measured whatever their grade. If the ruler changes, it is not a
ruler. It's something else.
Look at Figure 4. To obtain the arrangement in Figure 3 and to
keep it stable, we need a special kind of response curve. Here is
the item response ogive deduced from the standard definition of
measurement. These curves are parallel, in the sense that they
don't cross. If you make the vertical axis log-odds instead of
probabilities, you will find that these curves become straight
lines that are exactly parallel. The important thing to see is that
they don't cross each other.
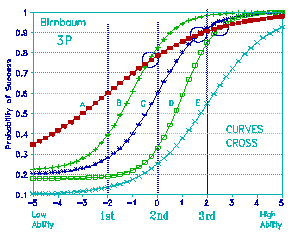
Figure 5. Five Birnbaum Curves and Three Ability Levels
1st = Low ability; 2nd = Medium ability; 3rd = High Ability |
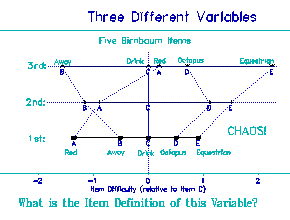
Figure 6. Five Birnbaum Items and Three Ability Levels
1st = Low ability; 2nd = Medium ability; 3rd = High Ability
Notice the 3 different item-difficulty hierarchies (advancing from left to right) |
Now let's see what happens when we look at some Birnbaum curves.
Figure 5 shows a handful of typical Birnbaum curves. They have
different asymptotes, different slopes. It looks messy. It doesn't
look like any measurement system that I would want to work with.
Why? Because the curves cross.
In Figure 6 we see the consequence for the variable experienced
by those three children. Incredible! Look at the 1st Grader. "Red"
is easier than "away" is easier than "drink" is easier than
"octopus". OK. But what happens to the 3rd Grader? For the 3rd
Grader its "away" that is easier. "Red" is harder even than
"drink"! And "octopus" is now next to "red", instead of up near
"equestrian". What is the definition of this variable? What is the
construct defined here? What kind of ruler is this? It changes for
every level of ability. I can't make a living with that kind of a
ruler. No scientist, engineer, businessman or cook, who depends on
measures of the kind this carpenter's ruler exemplifies, can work
with that kind of ruler.
Let's go backwards. Much as I might be intrigued by the apparent
sophistication of the Birnbaum curves in Figure 5, I cannot work
with them. I must have orderly, cooperating curves like the Rasch
curves in Figure 4, and I must find data that will serve this
purpose. I cannot swallow whatever junk happens to come my way. I
must be choosy and selective and careful when I construct my data.
When I go to market I don't buy rotten fruit. I buy good fruit.
When I make a salad, I only pick the parts that make a good salad.
I have a recipe for what I want. I have a model for
measurement.
I need to make the kind of a structure in Figure 3 - the same
ruler for everybody, so I can have a useful and stable construct
definition like Dick's word-recognition ruler in Figure 2.
The Birnbaum model is data-centered: model must fit, else get a
better model. It hardly ever objects to any item. The Rasch model
is theory-centered: data must fit, else get better data. And in the
search for better data, wonderful things are discovered about the
nature of what you are measuring and the way that people can tell
you about it. These discoveries are important events which develop
and strengthen your construct and your ability to measure it. The
Birnbaum model is patched up to chase after whatever pops up. The
Rasch model is derived a priori, to define the criteria
which data must follow to qualify for making measures.
Benjamin D. Wright
Barton, Marc A, & Lord, Frederic M. (1981) An upper asymptote
for the three-parameter logistic item-response model. Princeton,
N.J.: Educational Testing Service.
Birnbaum, A. (1968). Some latent trait models. In F.M. Lord &
M.R. Novick, (Eds.), Statistical theories of mental test scores.
Reading, MA: Addison-Wesley.
Guilford J. P. (1936). Psychometric Methods. New York: McGraw-
Hill.
Guttman L. (1950). The basis for scalogram analysis. In Stouffer
et al. (Eds.), Measurement and prediction. New York: Wiley.
Masters, G.N. (1988). Item discrimination: When more is worse.
Journal of Educational Measurement, (24), 15-29.
Stocking, M. L. (1989). Empirical estimation errors in item
response theory as a function of test properties. (Research Report
RR-89-5). Princeton: ETS.
Thorndike E. L. (1904) An introduction to the theory of mental
and social measurement. New York: Teachers College, Columbia
University
Thurstone L. L. (1925) A method of scaling psychological and
educational data. J Educ Psychol 1925; 15:433-51.
Woodcock, R. W. (1974). Woodcock Reading Mastery Tests.
Circle Pines, Minn: American Guidance Service.
IRT in the 1990s: Which Models Work Best? 3PL or Rasch? B.D. Wright … Rasch Measurement Transactions, 1992, 6:1, 196-200