Catching Copiers: Cheating Detection

For every pair of students (but you could reduce this by pairing only those who could have possibly cheated), plot "count of shared correct responses" against "count of shared incorrect distractors". This will produce a triangular empirical distribution. Outliers away from the triangle have both shared special knowledge and shared special ignorance - a strong indicator that they are not independent.

Unexpectedly similar strings of test responses by a pair of examinees need to be identified and diagnosed. Similarities can be caused by test-wiseness, curriculum effects, clerical errors or even copying.

Copying on a multiple-choice test can result in two very similar examinee response strings. They can also differ because of sloppy copying and copying only in part. Rasch fit statistics can detect similarity between an examinee's responses and the Guttman-pattern of expected responses, but they do not identify similar, non-Guttman, response strings. Both strings can show reasonable Rasch fit. The strings may also produce different ability estimates. How then can we expose response strings which are unacceptably similar?

Sir Ronald Fisher ("Statistical Methods and Scientific Inference" New York: Hafner Press, 1973 p.81) differentiates between "tests of significance" and "tests of acceptance". "Tests of significance" answer hypothetical questions: "how unexpected are the data in the light of a theoretical model for its construction?" Different models give different results. No result is final. Since observing two identical, but reasonable, response strings may be just as likely as observing two different, but reasonable, response strings, arguing for or against copying with a significance test can be inconclusive.

"Tests of acceptance", however, are concerned with whether what is observed meets empirical requirements. Instead of a theoretical distribution, local experience provides the empirical distribution. The "test" question is not "how unlikely are these data in the light of a theory?", but "how acceptable are they in the light of their location in the empirical distribution?"

For MCQ tests we can base our "test of acceptance" on the criterion of too many shared responses (right or wrong). Each response string is compared with every other response string. These pair-wise comparisons build an empirical distribution which describes this occasion completely. Acceptable pairs of performances define the bulk of this distribution. Outliers in the direction of too much similarity become unacceptably similar performances. Outliers in other directions indicate scanning misalignment, guessing, and other off-variable behavior.

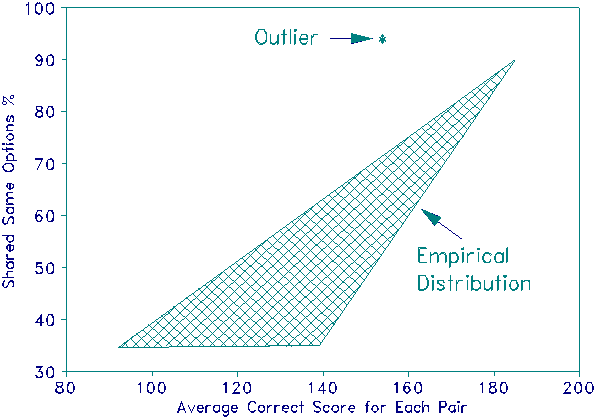
Diagnostic Plot of Unexpected Response Similarities

This "test of acceptance" can be implemented with a simple plot. Imagine 200 items taken by 1,000 examinees. When each examinee is compared with every other examinee there are (1000x999)/2 = 499,500 pair-wise comparisons. The percentage of possible identical responses, same right answers and same wrong options, to the 200 MCQ items will be between 0% (for two entirely differently performing examinees) and 100% (e.g., for two examinees who obtain perfect scores). It is not this percentage that is unacceptable, it is its relationship with the ability levels of the pair of examinees. The ability levels of the examinees can be represented in many ways. A simple approach is to use their average correct score to represent their combined ability levels. The Figure shows such a plot. Virtually all points representing pairs of response strings fall in a triangle, defining the empirically acceptable distribution. The "Outlier" point exposes a pair of examinees with an unusually large percentage of shared responses for their ability level.

"Correct" and "Incorrect" response similarities can be investigated separately. A plot of "same right answers" against average correct score exposes the acceptability of shared "correct" performance. A plot of "same wrong options" against the number of same wrong items (regardless of distractor choice) exposes the acceptability of shared "incorrect" performance.

Since copying is only one cause of highly similar response strings, a non-statistical investigation must also be done. Statistical evidence cannot prove copying. Nevertheless, inspection of this kind of empirical distribution does identify pairs of examinees with response strings so unusually similar that it is unreasonable to accept these strings as produced by the same response process which generated the other response strings.

John M. Linacre

Catching Copiers: Cheating Detection. Linacre J. M. … Rasch Measurement Transactions, 1992, 6:1, 201

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt61d.htm

Website: www.rasch.org/rmt/contents.htm