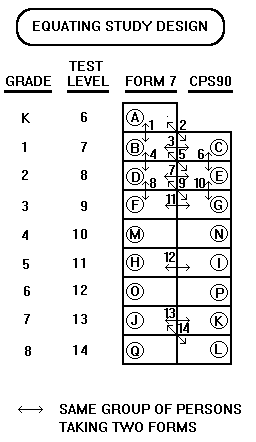
Figure 1. Equating Study Design
A study of student performance across grades K through 8 required the equating of 17 test forms for each of two curriculum areas: Mathematics and Reading. Advances in Rasch technology enabled this to be achieved through the construction of one response matrix for each area. I will focus on the Mathematics analysis.
 Figure 1. Equating Study Design |
17 test forms, comprising Levels 6 through 14 (Grades K through 8) of the ITBS Form 7, and levels 7 through 14 (Grades 1 through 8) of CPS90, were equated in one step. Figure 1 shows the equating design. Each lettered rectangle corresponds to one test form. Some students took only one test form in the usual way. Some students took two test forms to provide common-person linking. Each of the 14 arrows in Figure 1 indicates a group of 100 to 150 students who took two test forms marked by arrow ends. These are the common-person links between pairs of forms. The test publishers designed these test forms so that adjacent levels between levels 9 and 14 share common items. This provides "common-item" equating at the higher levels.
Valid equating of math forms requires data that capture the math variable. Data contaminated by guessing, response set or disinterest, must be set aside from an equating study and only be reintroduced later for diagnostic or individual reporting.
Irrelevant test behavior was "cleaned out" of these data in five stages. Set aside were: (1) Answer forms with scanning or marking problems: (a) more than three double-marked responses. (b) lightly marked forms with more than 1 blank response followed by non-blank responses. (c) very lightly marked forms.
(2) Response strings indicating extreme student disinterest or out-of-level testing: (a) more than 25% of the items left blank. (b) many identical responses: "response sets". (c) repeating patterns of responses.
(3) When each test form at each grade level was analyzed separately, response strings showing excessive off-variable behavior, i.e., with infit and outfit mean squares above 2.5.
(4) When infit or outfit mean-squares were above 2.5, and there were many standardized residuals 3 or larger (suggesting guessing or carelessness).
(5) When students took two test forms, and standardized differences between their pairs of measures were above 2, and responses in their lower test performance showed evidence of irrelevant test-taking behavior, e.g., many omitted responses, response sets.
Standardized differences were obtained by:
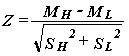 |
This cleaning set aside 12% of the data.
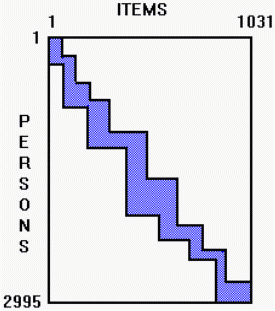 Figure 2. Matrix for Equating Forms |
The common-person and common-item links enabled all 17 test forms to be amalgamated into one block-diagonal "giant" matrix, shown schematically in Figure 2. Responses to different test items by the same person were aligned in the same row. Since many pairs of test forms had items in common, students often took the same item twice. In these cases, chronologically first responses were used. Responses to the same item by different persons were stacked in the same column.
Clerical mistakes were hard to avoid in setting up this equating design. Positioning the common items in the giant matrix required care. ITBS items are shared by two and sometimes three tests. Each different new item was assigned its own column in the matrix. When counting out columns, it proved easy to miscount. This threw subsequent item columns out of alignment. Sometimes miscounting went unnoticed until analysis reported the number of items to be different from that expected. When that happened, it was necessary to determine which columns were misplaced, and realign them.
Once the giant matrix was correctly constructed, it was analyzed by computer in the usual way. As discussed in RMT (5:3, p.172), obtaining good estimates from the block diagonal form of Figure 2, with 86% of the data missing, required fine convergence criteria. These criteria overcame the vertical-equating "range restriction" problems sometimes reported in the literature. Convergence required 263 iterations, 240 more than usual for a single test form. The decisive convergence criterion was the maximum marginal score residual. Convergence was not satisfactory until the largest marginal score residual was less than 0.5 score points.
The fact that all students and all test items were now part of the same connected data set, regardless of grade, test form or test publisher, enabled all student and item measures to be located on a single common scale of mathematics competency. The measures were then used for further investigation into such topics as the equivalence of test forms and the changes in math competency across grades.
Ong Kim Lee
MESA Psychometric Laboratory
University of Chicago
Calibration Matrices For Test Equating. Lee O.K. … Rasch Measurement Transactions, 1992, 6:1, 202-203
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt61e.htm
Website: www.rasch.org/rmt/contents.htm