Treatment Effects: Fixed-Effects Chi-Square of Homogeneity

Treatment effects, structural item properties, experimental conditions and time points can be modelled as constituents of item difficulty according to Gerhard Fischer and Ivo Ponocny (Annual Meeting of the Psychometric Society, Columbus, Ohio, July 1992).

This paper discusses a self-rating inventory of 24 items (symptoms of psychosomatic disorders) with 4 response categories, administered to 87 patients prior to and after treatment. 37 patients received medication and relaxation therapy, 50 only medication. Each patient is modelled at a constant level of functioning. New constituents are introduced into the item difficulties to mark changes in patient functioning after treatment. The model can be:

log_e(Pnimrj/Pnimrj-1) = Bn - Di - Mim - Rir - Fij

Bn is the functional level of person n
Di is the difficulty of item i
Mim is medication improvement
Mi1=0 prior to treatment
Mi2 is post-treatment benefit on item i
Rir is relaxation improvement
Ri1=0 prior to treatment, or for no-relaxation
Ri2 is post-treatment benefit on item i
Fij is the partial credit scale structure for item i.

The authors ask: Is the effect of medication, Mi2, (or relaxation, Ri2) the same for all items? Does it have a statistically significant effect on patient functioning? They base their answers on Conditional Maximum Likelihood estimation CMLE, because "likelihood ratio tests can be established rigorously and can easily be carried out". Likelihood ratio tests are valid when the hypothesis is true, the sample size is large and normality holds. Then differences between log-likelihoods become Chi^2- distributed. To test the hypothesis that Mi2 (or Ri2) are the same for all items, two analyses are performed. First the log-likelihood of the data under the full model is estimated, lambda1. Then Mi2 is reparameterized as M2, modelling a common medication effect across items, and a new log-likelihood estimated, lambda2. The test statistic is

Chi^2 = -2(lambda2 -lambda1)

with 23 degrees of freedom (24 item effects - 1 common effect). The hypothesis that M2=0 (or R2=0) can be tested in a similar way.

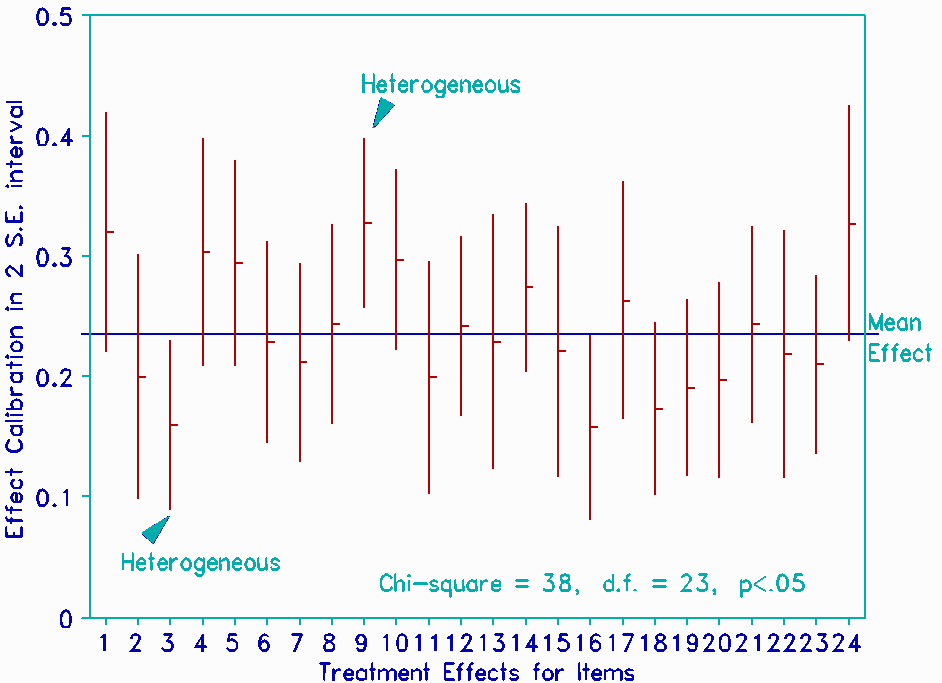
However, for any method producing a measure and standard error for Mi2 (or Ri2), the equivalence of treatment effects across items can be investigated with just one analysis, a "fixed effects" chi-square of homogeneity [see Box].

A graphical version of this is to plot the estimates of Mi2 (or Ri2) with 2 standard-error confidence bands. When all confidence bands overlap the common effect, then the estimates are statistically equivalent. An estimate of this common effect is the information-weighted mean of all item-level effect estimates [see Box]. The arithmetic mean is good enough when standard errors of item-level effects are similar.

A simple way to obtain the common effect of Mi2 (or Ri2) is to reanalyze the data parameterizing those common values as M2 (or R2). A t-test of the hypothesis that there is no M2 (or R2) effect is obtained by dividing M2 (or R2) by its standard error.

These approaches to estimating the size and statistical significance of effects yield slightly different numerical results, some more approximate than others, none absolutely precise. This reminds us that it is the meaning of numbers, not their values when compared to arbitrary criteria, that is paramount.

Treatment Effects

Treatment Effects: Fixed-Effects Chi-Square of Homogeneity, J Linacre … Rasch Measurement Transactions, 1992, 6:2 p. 218-9

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt62b.htm

Website: www.rasch.org/rmt/contents.htm