Hambleton's 9 Theses, R Hambleton et al.

During Ronald K. Hambleton's opening statement in the AERA debate, "IRT in the 1990s: Which Models Work Best," he advanced nine theses to support the use of two- and three-parameter (3-P) IRT models. In the debate, the opening statements of Ben Wright and Hambleton were followed by discussion from Linda Crocker, Geoff Masters and Wim van der Linden, further remarks by Wright and Hambleton, and then comments from the audience of several hundred, moderated by Gwyneth Boodoo. Here is a summary of Hambleton's nine theses with other participants' commentary.

Thesis 1: At least 50 years of 3-P development.

In the 1940s the sample-dependent nature of "true-score" item and ability parameters motivated the search for parameter invariance. In 1952-3, Frederic M. Lord's investigation of item characteristic curves (ICCs) culminated in the normal-ogive model, incorporating both difficulty and discrimination parameters. In 1957-8, Birnbaum replaced the normal ogive by the logistic ogive function and added a "guessing" parameter. Rasch's work became known in 1960, but Lord had already rejected that model due to its inferior fit to his data.

Commentary: Louis Thurstone, concerned with parameter invariance, published an "absolute scaling" method in 1925. IRT came into existence with the widespread use of MCQ tests, and, in its 3-P form, will not survive the imminent demise of MCQ. Rasch's models are designed to construct linear measures from qualitatively-ordered observations. Model-data misfit raises more questions about the data than the model.

Thesis 2: The model must fit the data.

Scientists develop models to explain or fit their data, not the reverse. Georg Rasch wrote: "That the model is not true is certainly correct, no models are." To discard items or persons that are not consistent with the model is not defensible. Curriculum specialists can not be asked to narrow their test content for the sake of a psychometric model.

Commentary: Models are not designed to be true, but to be useful. Since most parameter estimates are used in statistical techniques intended for linear quantities (e.g., addition, subtraction, means, regressions), models that produce linear measures are more useful than models that merely describe a particular data set numerically. When MCQ data do not fit the Rasch model, these particular data cannot support linear measurement or the use of statistics designed for linear analysis.

The Rasch model does not require that any data be discarded or that any tests be narrowed. It does, however, alert test constructors to mis- keyed items, lucky guessing, and heterogeneous item content, all of which are not consistent with the linear measurement of one latent trait. Test constructors are then free to take whatever action they wish.

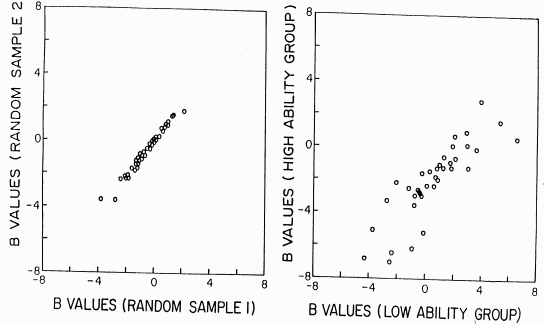
Thesis 3: Parameter invariance.

Since 3-P and Rasch models are non-linear regression models, any reasonably heterogeneous sample of data points can yield invariant parameter estimates. In practice, invariance requires an appropriate data collection design, the model to fit the data, and parameters to be estimated properly. Though invariance is never observed in the strict sense, the degree to which it holds can be assessed through plotting estimates of the same parameters from different samples. A large amount of scatter indicates model-data misfit or poor parameter estimation.

Stability of IRT item difficulty parameters. From Hambleton RK, Rogers HJ (1988) Solving criterion-referenced measurement problems with item response models. NCME-AERA, New Orleans

Commentary: Parameter invariance is a theoretical property. For data that fit the model, 3-P estimates more parameters than Rasch. Consequently, once a set of parameter estimates has been obtained, parameter invariance necessarily imposes more constraints on the next sample of data for 3-P than for Rasch. 3-P may on occasion describe one sample of data more completely than Rasch, but 3-P is far less robust then Rasch against secondary changes in data characteristics (e.g., additional test items, different examinee distributions, missing data).

Thesis 4: Item discrimination.

80 years of test construction tell us that variability in item discrimination is inevitable and is different from multi- dimensionality. Two arguments for an item discrimination parameter are (1) you don't want to eliminate some of your best items, and (2) removal of non-fitting items changes the nature of the test. It is true that item discrimination prevents the computation of sufficient statistics, but these are not essential. Even for the Rasch model, they only have value to the extent that the model fits the data. More important is the maximization of test information through the use of item scoring weights based on item discrimination. In recent Dutch research, imputed item discrimination was found to be a useful addition to the Rasch model.

Commentary: Variability in item discrimination, though inevitable, is not desirable. In the form of point-biserials, this variability has been used as evidence of item misfit for 60 years. Construct validity requires that the test look the same regardless of the ability of the examinee. Variability in item discrimination requires ICCs to cross, meaning that the difficulty ordering of the items is dependent on the ability of the examinee. Items with low discrimination cannot detect the difference between high and low ability, so are of little value to measurement. Highly discriminating items show not more information, but more redundancy with the rest of the items, the infamous "attenuation paradox". Their high correlation with the rest of the test implies that they contribute less than their share of new information about examinee performance. The Rasch model is flexible enough to encompass what most test developers regard as a reasonable range of item discrimination variability across items in one test. Imputed, i.e., "pre-set", discrimination values imply that there are reasons, outside the data, for differences in item discrimination that are in accord with linear measurement. Again, Rasch models are flexible enough to handle such situations, when there is a sound reason for them.

Statistical sufficiency is a useful Rasch property. It simplifies parameter estimation. But the primary argument for Rasch is the construction of measures that are linear by reason of conjoint additivity and objectivity ("sample-free" and "test-free" parameter separability). 3-P parameter estimates do not actually have linear properties. They are merely asserted to be linear because they are expressed numerically.

Thesis 5: Pseudo-Guessing Parameter.

Accounting for the non-zero item performance of low ability candidates improves model fit. Proper choice of examinee sample, estimation of a common value for all items, and Bayesian priors improve estimation of these parameters.

Commentary: The inclination to guess is an idiosyncratic characteristic of particular low ability examinees. Lucky guessing is a random event. Neither feature contributes to valid measurement of a latent trait. Parameterizing guessing penalizes the low performer with advanced special knowledge and also the non-guesser. Rasch flags lucky guesses as unexpected responses. They can either be left intact which inflates the ability estimates of the guessers, or removed which provides a better estimate of the guessers' abilities on the intended latent trait. In practice, 3-P guessing parameter estimation is so awkward that values are either pre-set or pre-constrained to a narrow range.

Thesis 6: 3-P Software works!

As is usual in numerical analysis, 3-P software incorporates constraints on parameters, prior beliefs, and sensible starting values. Convergence problems, multiple maxima, and other technical characteristics of 3-P programs are well documented and controlled. These programs work quite well under reasonable conditions of test length and sample size. They work well with moderately long tests and large sample size. Problems with Rasch programs include statistical bias in estimates, questionable fit statistics and lack of technical documentation. Problems common to both Rasch and 3-P programs include omitted responses, item context effects, and parameter estimation for the new multi-parameter extended models.

Commentary: 3-P programs are hard to use and require data set sizes and other resources much beyond most testing agencies. Martha Stocking (1989) reports once again on the severe difficulties encountered even in recovering generating parameters for simulated 3-P data. The statistical bias in some, but not all, Rasch estimation algorithms is well documented, is always far less than a standard error, and is negligible in tests longer than 20 items. Rasch parameter-level fit statistics are well documented and are only questionable in the sense that empirical parameter distributions never match theoretical distributions exactly. Parameter level fit statistics are seldom reported for 3-P. Current Rasch software easily handles omitted responses and parameter estimation for extended models. Item context effects are diagnosed through Rasch fit statistics, and can be explicitly modelled through polytomous techniques.

Thesis 7: Successful use of 3-P.

The National Assessment of Educational Progress (NAEP), CTB/McGraw-Hill, LSAT, GMAT, SAT, GRE and TOEFL use 3-P in test design, item bias, score equating, etc. Rasch proponents overstate problems with 3-P.

Commentary: Most claimed applications of 3-P use pre-set or very narrow ranges of item discrimination and pseudo-guessing parameter values. These constraints cause 3-P to approximate 1-P, i.e., Rasch estimation. In most reporting, examinees with the same raw score all receive the same standardized score, eliminating entirely any supposed benefits of item discrimination weighting. Though substantial academic and professional activity and prestige has promoted 3-P for 40 years, the fact that 3-P has yet to motivate any improvement in test construction or to illuminate the understanding of any latent trait exposes its total impotence as a scientific method.

Thesis 8: Rasch model deficiencies.

In addition to those mentioned above, vertical equating problems.

Commentary: Technically, vertical equating is no longer a problem. The ease with which Rasch software handles missing data enables multiple test forms and administrations to be included in one comprehensive analysis. Problematic to any equating method, however, are changes in item difficulty (e.g., due to learning effects) and changes in the nature of the latent variable across grades.

Thesis 9: Promising future of 3-P and descriptive IRT.

Polytomous 3-P models and multidimensional models are under development, as are models incorporating psychological and cognitive theory. Diagnostic reporting on individual and group levels is coming. New item formats, scoring schema, and test contents should not be narrowed to fit Rasch models. Rasch has an important role only when 1) it fits data well, and 2) sample sizes are modest with no need for highly precise estimates.

Commentary: The arrival of "authentic assessment" raises new challenges for testing and measurement. New models are definitely needed. More complex situations require yet more careful conceptualization if confusion is to be avoided and progress made. A multidimensional test score, which combines performance on two or more different latent traits simultaneously, is inevitably ambiguous and confusing. A useful paradigm is that of observation => measurement => analysis. The observation model collects qualitative manifestations (successes, ratings, frequencies) of one latent trait at a time. The measurement model converts these qualitative observations into linear quantities. The analysis model constructs knowledge out of the relationships among the linear measures derived from many observation models. Rasch is already operating in this way in a broad spectrum of testing situations on a wide variety of new item formats and scoring schema in data sets of all sizes, and thence facilitating deeper understanding of latent traits through comprehensive diagnostic reporting.

Stocking ML. 1989. Empirical estimation errors in item response theory as a function of test properties (Research Report 89-5). Princeton NJ: Educational Testing Service

Hambleton's 9 Theses, R Hambleton et al. … Rasch Measurement Transactions, 1992, 6:2 p. 215-7

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt62d.htm

Website: www.rasch.org/rmt/contents.htm