Variance in Mathematics and Reading across Grades: Grade Equivalents and Logits

Does schooling make students more alike or more different? In 1916, Woody assumed within-grade variance in student performance to be constant across grades for his arithmetic tests. Thurstone, however, reanalyzing Woody's data in 1928, reported a "striking increase in absolute variability through the grades." A widely held view is that: "Variability is lowest in the lowest grades, when children are uniform in beginning their education. In later, grades, some have progressed much more than others, and the variability increases markedly" (Hills, 1976, p. 163).

A recent Rasch equating study of the Iowa Test of Basic Skills (forms CPS90 and CPS91) for math and reading, based on a cross-sectional sample of students in Grades 1 through 8 from the Chicago Public Schools, sheds light on this question.

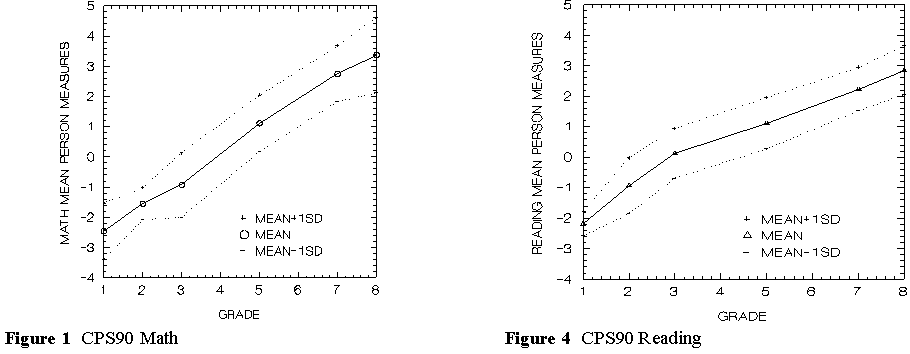
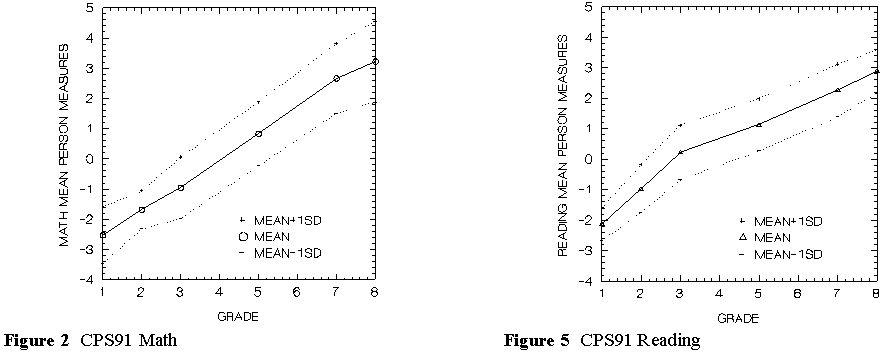
The Figures show plots of person measures in each grade. Increase in ability in math, Figures 1 and 2, is fairly uniform across grades. This constant increase in math ability is not surprising because math learning does not approach a ceiling during a student's school career. There is always more math to learn.

Reading ability, Figures 4 and 5, however, increases more rapidly than math up to the third grade and thereafter more slowly.

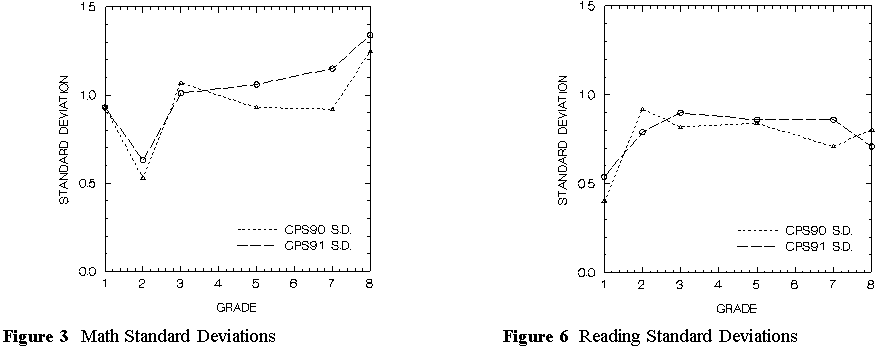
Figures 3 and 6 show how the standard deviations of the person measures in math and reading vary with grade. We expect students from various backgrounds to begin school with varied abilities in subjects for which they have not had formal instruction such as math. As they progress in the grade, however, we expect students to become more homogeneous as they learn and practice on a subject. This will continue until a new topic is introduced. Then students can be expected to disperse.

Figure 3 implies that new math topics are introduced in the third grade. Students' math ability standard deviation decreases in the second grade as addition and subtraction are mastered, but increases in the third grade as long division looms. The math standard deviation then remains somewhat constant for grades 4 through 7, increasing slightly in grade 8.

Reading, on the other hand, reaches a steady state for most children. New words may be learned in each grade, but styles, techniques, and methods remain the same. As students move up in the grades, their reading standard deviations can be expected to decrease. Students begin their formal instruction on reading in the first grade. It is not surprising to see their standard deviation going up slightly by second grade. This can be seen in Figure 6. But, after the second grade, reading standard deviation begins to decrease.

Hills JR 1976 Measurement and Evaluation in the Classroom. Columbus, OH: Charles E. Merrill

Thurstone LL 1928 Scale construction with weighted observations. Journal of Educational Psychology 19, 7, 441-453.

Variance in Mathematics and Reading across Grades: Grade Equivalents and Logits, O K Lee … Rasch Measurement Transactions, 1992, 6:2 p. 222-3

Please help with Standard Dataset 4: Andrich Rating Scale Model

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt62f.htm

Website: www.rasch.org/rmt/contents.htm