Mean-square Significance and Sample Size

An investigation of item fit is central to the selection of items. Item misfit to the Rasch model can be summarized in mean-square statistics. Associated with each mean-square is a significance level based on a test of the hypothesis: "Responses to this item fit the model perfectly." All significance tests, however, are sensitive to sample size. While power in significance testing can be worthwhile, "too much power" due to exceedingly large samples may lead to faulty conclusions about item fits.

Experimental versions of an anatomy examination were administered to 4998 individuals. Due to the resulting power of the hypothesis test, 29 of 47 items showed significant statistical misfit (p<.05), creating the impression that many items were unusable. Though each item will ultimately be examined for other aspects of quality, such as discrimination and guessing, it is useful to have a more realistic indication of fit and misfit than the conventional significance levels.

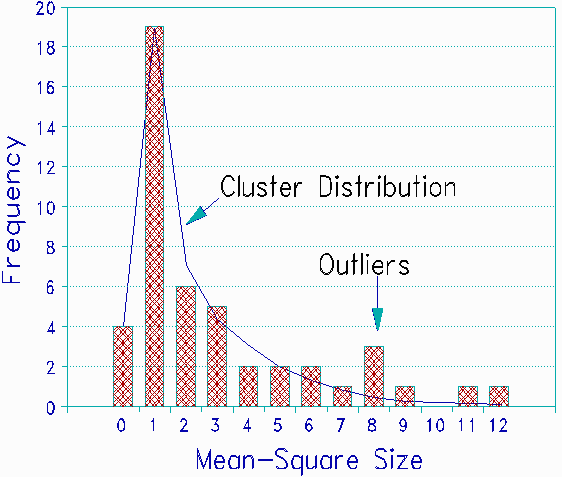
A first step is to examine how the mean-square values distribute. This distribution provides insight into whether or not the items are functioning in a similar way. In a histogram of the mean-square statistics we expect a pattern in which many statistics are clustered around a central location (near 1.0) while others are "outliers". Items in the cluster are exhibiting similar fit. Outliers are divergent. When the mean-square fit statistics for the anatomy items are plotted, the expected cluster emerges near 1. This cluster includes all the "good" fit items, based on their statistical significance, and half of the "bad" items. Since the mean-squares are ratio scale statistics, the "cluster distribution" drawn into the Figure was obtained by fitting a smooth symmetric curve to the logarithms of the mean-squares, and exponentiating back to the ratio scaling.

This result does not mean that all items in the cluster should be immediately accepted into the final version of the examination. Nor does it mean that those outside the cluster be rejected. Rather this information provides an orderly basis for choosing final item sets.

Mean-square distribution

Mean-square Significance and Sample Size, P Halkitis … Rasch Measurement Transactions, 1992, 6:3 p. 227-8

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt63a.htm

Website: www.rasch.org/rmt/contents.htm