Combining and Splitting Categories: Collapsing Categories

Rasch measurement is constructed from counts of the presence (or absence) of indicative events that are classified into ordered categories. "The categories can be thought of as contiguous intervals on some continuous scale" (McCullagh 1980 p.110). For a dichotomous item, there are two categories: present/ absent, yes/no, right/wrong. For polytomous items, there can be many categories: none/some/many/all. For Poisson items, there are the unlimited number of categories: 0/1/2/ etc.

McCullagh (1985 p.39) advises: "If a model is to be used as a basis for understanding or inference, it must have a plausible scientific basis... While it may be necessary, it is not sufficient to choose a model solely because it fits the data well: adequate attention must be paid to the processes by which the data might have been generated."

To use this advice, it is necessary to distinguish three components in McCullagh's one term, "model":

1) "The processes by which the data might have been generated", i.e., the Observation Model that defines what is counted. The category classification rules are Observation Models.

2) "The model .. to be used as a basis for understanding and inference", i.e., the Measurement Model that specifies how counts of qualitative observations are to be converted into measures suitable for quantitative analysis.

3) The "model [that] fits the data", i.e., the Analysis Model that describes and summarizes the measures.

The Observation Model, which defines categories and assigns observations to categories, always entails the arbitrariness of choice, judgment, decision and compromise. What is a "correct" response to the question: 2+2=? Most would say 4. But why not 11? Because a decision has been made that addition shall be base 10 and not base 3. Are 4.0 or 3.999 also acceptable? These results are produced by many computer programs.

Arbitrariness becomes more obvious as the number of categories increases. Are attitudes best recorded as agree/neutral/disagree or strongly agree/agree/disagree /strongly disagree?

This arbitrary nature of rating scale definitions has implications for the practice of measurement. There are three schools of thought about how much Observation Model manipulation is valid:

School 1) Regard the Observation Model as entirely rigid (an inviolable commandment):
Whatever rating scale the test designer happened to begin with is forever the "correct" one. This rating scale must be accepted or rejected as a whole. Any attempt to split or combine (collapse) categories loses the definition of the scale initiated by the scale's designer and therefore used by the respondents.

School 2) Regard the Observation Model as entirely flexible (a passing whim):
Since categories are arbitrary, "it is nearly always appropriate to consider models that are invariant under the grouping of adjacent response categories" (McCullagh 1985 p.39). If all categories remain ordinal, how they are lumped together is irrelevant. The only statistical model with this property is the "Graded Response Model" of Thurstone and Samejima.

School 3) Regard the Observation Model as subject to exploration and hence modification (a device for developing knowledge):
The categorization of a scale is inevitably arbitrary, but also informative. The scale designer may have done a good or poor job of scale definition. The respondents may have used the scale effectively or ineffectively, according to their own understandings of the category labels. But even the most careful choice of category definitions may not be definitive. Klockars & Yamagishi (p. 86) describe how the choice of verbal labels for ordered categories focusses the respondents attention on different parts of the responses continuum, but, they caution, "when the labels attached to the response options are selected to saturate one end of the response continuum [to provide increased discrimination in that part of the scale], the meaning of the label and the meaning of the location in which the label is used on the continuum will be discrepant. The rater must somehow weigh the importance of the position and the label in deciding on a meaning of the options." It becomes the analyst's task to extract the maximum amount of useful meaning from the responses observed - combining (or even splitting) categories as suggested by the results of careful analysis.

Consider Guilford's (1954) data set. Three respondents make ratings on a 9-point scale. One respondent uses the 5 odd-numbered categories exclusively, another respondent uses the 5 odd-numbered categories and only one of the even numbered categories. The third respondent focusses his responses in the center of the scale, not using the extreme categories. Guilford, following School 1, analyzed the original numerical observations as though the scale were "correct" and also linear.

Clearly, the original definition of the scale in 9 numbered, but otherwise undefined, categories has failed. Since no respondent uses more than 7 categories, it seems that the respondents did not perceive 9 levels of performance. To analyze the scale as though the respondents conceptualized 9 levels of performance is to deceive ourselves. The choice forced on us by School 1 is to reject the entire scale and all of the data.

These data also fail to meet the requirements of School 2. The data must be rejected because different groupings of the 9 categories do not produce acceptably invariant results.

When considered from the viewpoint of School 3, however, the "processes by which the data might have been generated" can be taken seriously. Meaningful rating scales can be established for each respondent by combining observations differently for each rater. This approach leads to useful and coherent results.

The observation model cannot be considered in isolation. It must be considered in combination with a measurement model. The strongest bases for inference are linear measures that are "objective", i.e., as "sample-free" and "test-free" as possible. Such measures are produced from ordinal observations only by implementations of the unidimensional polytomous Rasch model (UPRM), such as Andrich's Rating Scale Model and Masters' Partial Credit Model.

Jansen & Roskam (p.429) discover that "data satisfying the UPRM, with a certain number of categories, will not do so [in general] when response categories are joined." Andrich (1992) agrees, saying that "if data do conform to the [UPRM] with one set of categories, then the same data will not conform to the model if adjacent categories are collapsed in any way... This result is, in fact, consistent with both linguistic theory [that the meanings of words depend on their context], and chaos theory [that measurement size is affected materially by measurement precision]. The construction of [UPRM] emphasizes how the ordered categories are not only defined according to their operational characteristics, but also simultaneously in terms of each other."

Thus some categorizations yield measures of higher quality than other categorizations. But, if we are to have a firm basis for further analysis (the analysis model), we must construct measures with optimal properties. So, if we are to take any observed phenomenon seriously, we cannot regard the definition of ordered categories as totally arbitrary.

Andrich (in McCullagh, 1980, p.15) instructs the analyst to dig yet deeper and investigate even the ordering itself: "therefore, may I suggest that models [such as UPRM] which permit the categories to reveal themselves to be ordered or otherwise, rather than those which constrain the categories to be ordered, may be more instructive for fully understanding certain types of ordinal variables."

These considerations force us to School 3. The analyst examines the data and recodes the observations to improve both the statistical and substantive validity of the results. In practice, alternative reasonable recodings of the responses often show equivalent fit of empirical data to UPRM and yield equivalent results -an encouraging outcome for those who are concerned lest their conclusions be based on a perhaps unreplicable set of accidents in the data.

In 1987, Wright suggested the following empirical rules for joining adjacent categories for UPRM:

1) Be sure whatever joins are contemplated make sense! If you decide to combine two or more adjacent categories, be sure you can explain why it is entirely reasonable to think of these joined categories as signifying the same level of your basic variable.

2) Do not exceed the number of modal (most probable) categories in the original categorization. The number of modal categories brings out the number of qualitative segments on the variable this sample of persons perceived in these items. Grouping several rarely-used categories together can artificially construct a new modal category. Remember that the way in which modal categories are selected in a rating scale can be sample-dependent, even when data fit UPRM.

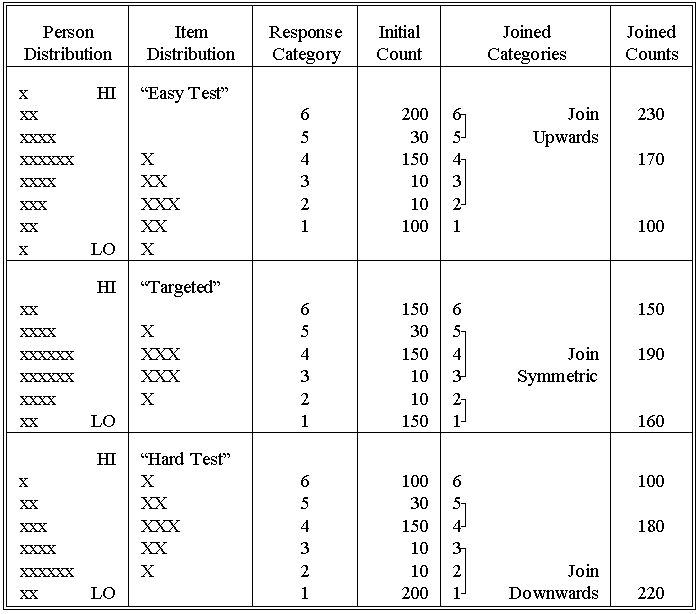
3) Construct a category frequency histogram with face validity. Join categories so that their frequency profile matches the distribution profile of the relevant segment of the sample of persons:

a. When the sample distribution histogram is rising toward measures near the mean item difficulty, as it will for tests that are "easy" for the sample, join categories so they increase in popularity upward toward the highest category.

b. When the sample histogram is peaked, goes up and then down, near the mean item difficulty, as it will for tests targeted at the sample mean, join categories so that they first increase and then decrease in popularity.

Should the sample histogram be more or less level near the mean item difficulty, join categories so that they are equally popular.

c. When the sample distribution histogram is falling toward measures near the mean item difficulty, as it will for tests that are "hard" for the sample, join categories so they decrease in popularity upward toward the highest category.

Splitting Categories

A single Observation Model category label, e.g., "Dissatisified", must be split into two Scoring Model categories when the label has two distinct, perhaps even opposite, meanings, e.g., "Dissatisfied because too little.." and "Dissatisfied because too much..". This occurs intentionally with folded scales, but sometimes with apparently hierarchical category labels. Splitting requires the imposition on the data of a substantive theory about patterns in the observations indicating whether each particular observation signifies "too little" or "too much" of the variable.

Note: Later work has shown that the observed person measure distribution for each category is also important in making combining and splitting decisions.

Andrich D (1992) On the function of fundamental measurement in the Social Sciences. International Conf on Soc Sci Methodology, Trento, Italy, June 1992.

Jansen PGW & Roskam EE (1984) The polytomous Rasch model and dichotomization of graded responses. p. 413-430. in E. Degreef & J. van Buggenhaut (Eds), Trends in Mathematical Psychology. Amsterdam: North-Holland.

Klockars AJ & Yamagishi M (1988) The influence of labels and positions in rating scales. Journal of Educational Measurement, 25, 2, 85-96

McCullagh P (1980) Regression models for ordinal data. J. Royal Statist. Soc B, 42, 2, 109-142

McCullagh P (1985) Statistical and scientific aspects of models for qualitative data. p.39-49, in P. Nijkamp et al. (Eds), Measuring the Unmeasurable, Dordrecht, The Netherlands: Martinus Nijhoff.

Illustration of guidelines for combining categories

Combining (Collapsing) and Splitting Categories, B Wright & J Linacre … Rasch Measurement Transactions, 1992, 6:3 p. 233-5

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt63f.htm

Website: www.rasch.org/rmt/contents.htm