Fred Mosteller and John Tukey (M&T) untangle many problems in "Data Analysis and Regression" (2nd Ed. Reading, MA: Addison-Wesley, 1977). Occasionally, however, they lose sight of meaning. M&T's Exhibit 11, Chapter 11, also printed on the book's back cover, is an example.
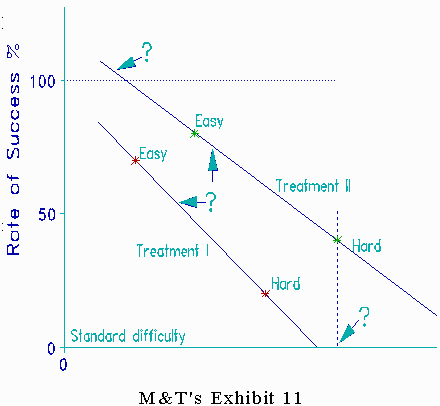
Exhibit 11 plots the success rates of two treatments on non-equivalent "Easy-to-treat" and "Hard-to-treat groups. M&T describe techniques for equating the groups that result in locating the four treatment groups on an infinite linear "standard" scale of treatment difficulty, the X-axis in M&T's Exhibit 11.
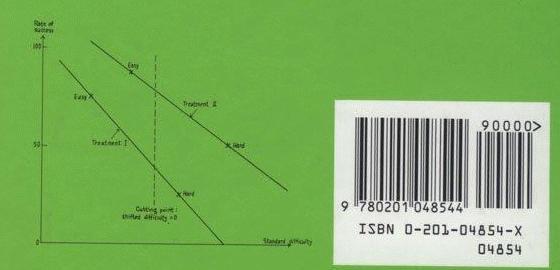
M&T's plotting of "Rate of success %" on the Y-axis, however, clouds the meaning:
1) M&T extrapolate Treatment II's regression line beyond 100% into the unobservable. What can this regression line mean?
2) M&T plot a straight regression line that maps a finite "Rate of Success %" scale onto an infinite "Standard difficulty" scale. This implies that, as patient groups get "harder", they soon intercept zero and so have no chance of successful treatment. Also, as patient groups get "easier", they become certain to be treated 100% successfully, but this is clearly unachievable. Indeed, are we to infer from this plot that no patients in the "hard" group of Treatment II could have been successfully treated by Treatment I?
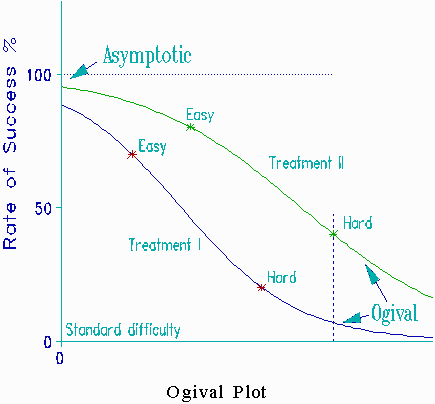
Rescaling "Rate of success %" to "Log-odds of success" in the "Log- Odds" plot solves both problems. This plot looks like M&T's Exhibit 11, but has infinite range on both axes. Now the regression lines are meaningful everywhere.

This can be seen in the "Ogival" plot that transforms the linear log-odds Y- axis back to the ogival "Rate of success %". The ogives do not exceed the 100% success rate limit. They do not predict unrealizable treatment success or failure. A meaningful rate of success with Treatment I can now be predicted for the "hard" group of Treatment II.