Probabilistic Mapping

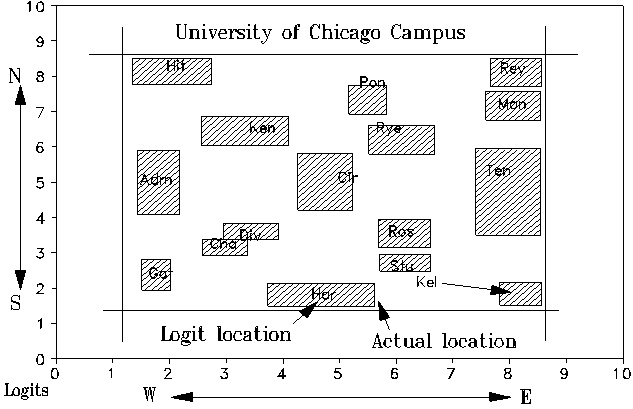
Is a probabilistic logit-based distance anything like a physical distance? Is our conceptualization of a "distance along a variable" merely fanciful? As a test of the congruence of these two ideas of "distance", I ambled around the University of Chicago campus among its familiar buildings and landmarks. Every so often, I paused to note down how far away from me I thought each landmark was, first north or south and then east or west, using a rating scale of apparent distance. On completing my walk, I had two rectangular data matrices with 16 landmarks along one side and the locations of my 30 pauses along the other. In one matrix, each cell contained a north-south distance rating. In the other, an east-west rating. The rating scales were crude. The east-west scale was: very far to the east (0), far to the east(1), near to the east (2), very near to the east (3), very near to the west (4), near to the west (5), far to the west (6), and very far to the west (7). I used a similar scale along the north- south axis.

Could Rasch analysis construct a campus map from these matrices?

Rasch analysis of each matrix yielded a logit distance for each landmark along each axis. These pairs of logit measures are plotted against each other in the Figure (in printed text) and marked by the first three letters of the name of the landmark. In the top left corner, Hit (Hitchcock Hall) was estimated to be at 8.32 logits to the north and 2.14 to the east. This provides a probabilistic location for the building. The building's actual location is marked by the X.

The probabilistic map matches the actual map, but requires an empirical linear transformation between logits and yards. This transformation is not the same for the two axes. The north-south axis is compressed relative to the east-west axis. It seems I was more discriminating in rating along the north-south axis than the east- west. Perhaps my perception was distorted because the campus is 50% longer east-west than north-south.

Overall, the Rasch model has successfully translated my vague notions of "far" and "near" into distances. The only misplaced building is Kel (Kelly Hall) at bottom right. It is too far to the west. Kelly Hall is also the only building with ratings displaying significant misfit. Looking at its ratings, I found that I had made glaring mistakes, falsely recording four ratings intended to be "far east" as "far west". I had become careless toward the end of my journey and reversed the directions. Fortunately, the method is so robust that Kelly Hall is misplaced only slightly.

The purpose of this experiment was not to discover the layout of the University of Chicago quadrangles. It was to check whether the logit "distances" calculated by the Rasch model for sociological variables, such as attitude, are analogous to physical distances. My informal experiment supports the theory-based proposition that they are (Fisher 1988 2:394). There need be no difference between the mathematics of social science and the mathematics of ordinary geometry. The two can be made to coincide by means of the Rasch model.

Moulton MH. (1993) Probabilistic mapping. Rasch Measurement Transactions, 7:1 p.268-9

Fisher W. P., Jr. (1988) Truth, Method, and Measurement: The Hermeneutic of Instrumentation and the Rasch Model. U. of Chicago dissertation.

Probabilistic mapping. Moulton MH. … Rasch Measurement Transactions, 1993, 7:1 p.268

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt71b.htm

Website: www.rasch.org/rmt/contents.htm