DNA Fingerprinting

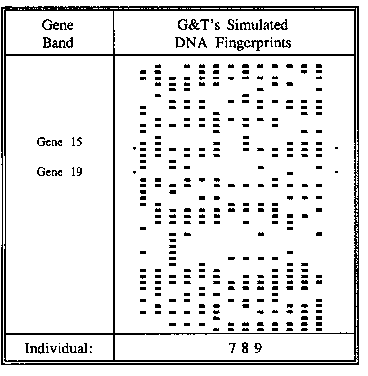
A DNA "fingerprint" provides a profile of an individual's genes. Researchers use this information to estimate how closely related individuals are. Geyer and Thompson (G&T, 1992) remark that previous statistical models have omitted important parameters "because without a stochastic model to guide inference, it is difficult to know what to do with them." G&T see the value of sufficient statistics for this problem and construct an autologistic model for DNA data that nearly gives Rasch measures. Here is a revision of their model that does provide Rasch measurement.

G&T's simulated DNA data for 13 individuals is illustrative (see Table). A "-" indicates the presence of the gene in the individual. Some genes are more widespread in the sample than others. Some individuals have more different genes and so are more genetically diverse than others. Individuals who share more genes are hypothesized to be more closely related. This is the basis of G&T's model, which can be expressed in Rasch form as:

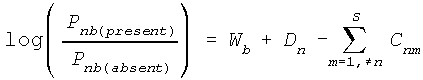Pnb(present) is the probability that individual n exhibits gene b.
Wb is how Widespread gene b is in the sample.
Dn is the genetic Diversity of individual n.
Cnm is the Closeness of the relationship between individuals n and m among the S individuals.

This model, as it stands, does not provide unambiguous measures because the individual's own genetic diversity cannot be disentangled from that due to relationships with others. This obstacle is overcome with a two-stage approach. First, as much genetic variation as possible is explained by the main effects - the measures of the prevalence of each gene and of the genetic diversity of each individual. Thus,

Then, these main-effect, Wb and Dn, measures are fixed (anchored) at their estimates, and the remaining variance is modelled as interactions, i.e., paired relationships among the individuals in the sample:

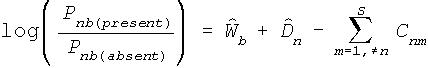This approach produces the plotted results. Gene 15 is exhibited by all but one individual. Individual 7 has the fewest different genes. Individuals 7 and 9 are the most closely related, because 9 exhibits all of 7's genes.

Linacre JM (1993) DNA Fingerprinting. Rasch Measurement Transactions, 7:1, p. 274.

Geyer C.J. & Thompson E.A. 1992 Constrained Monte Carlo maximum likelihood for dependent data. Journal Royal Statistical Society, B, 54(3), 657-699

--------------------------------------------------- Logit Gene Band Individual Pairing Prevalence Gene Mix Relation --------------------------------------------------- Widespread Diverse Close 3 7-9 15 *** 2 *** *** 1 ** ******** ******* ************** 0 **** 8 *** *************** ****** 9 ****** ** -1 ***** 8-9 * ** 7 ***** -2 19 ** (* = 2 pairs) -3 Rare Inbred Distant ---------------------------------------------------

DNA fingerprinting. Linacre JM. … Rasch Measurement Transactions, 1993, 7:1 p.274

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt71f.htm

Website: www.rasch.org/rmt/contents.htm