Rasch-based Generalizability Theory: Reliability and Precision (S.E.) Nomogram

Cronbach's Generalizability Theory (G-Theory) is "a technique for estimating the relative magnitudes of various components of error variation and for indicating the most efficient strategy for achieving desired measurement precision." (Shavelson & Webb, 1991, back cover). G-Theory is not concerned with fairness to examinees (e.g., adjusting scores for judge leniency) or with judge rating quality (e.g., idiosyncrasies, response sets). It is concerned solely with the relationship between the sought-for "true" variance in what is observed and the other unwanted main effect, interaction, or random error variances. G-Theory applies Fisher ANOVA to raw scores to estimate variance components and so compute reliability coefficients.

First, a pilot data collection is undertaken for a Generalizability Study (G-Study). Variance components for all main, interaction and random effects are estimated from these pilot data. These variances are asserted to be those that will occur in a future, more comprehensive data collection, the Decision Study (D-Study). Then a D-Study is designed to obtain a desired level of reliability based on the G-Study variance components.

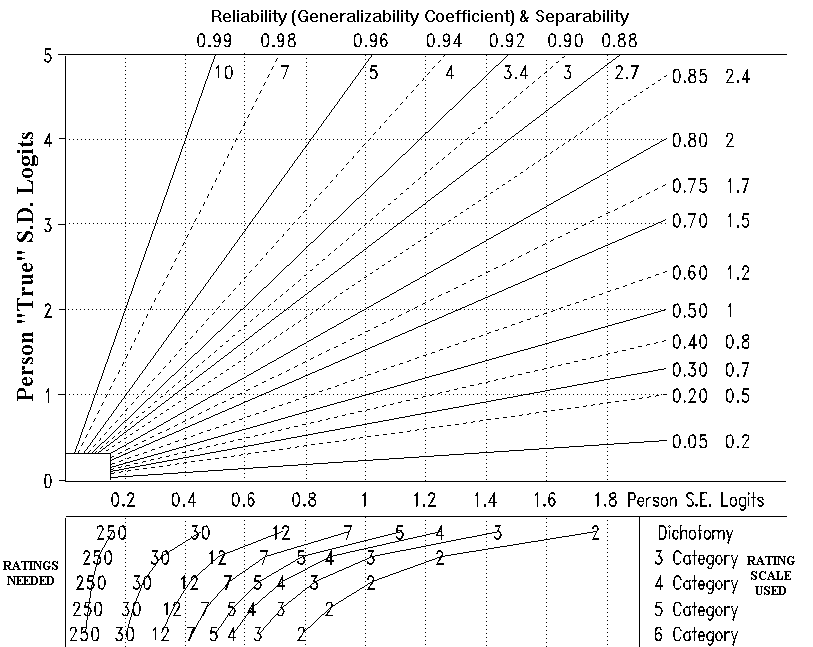
Rasch-based G-Theory has several advantages. First, no preliminary G-Study is needed. The precision (standard error) of an element's measure can be predicted solely from the number of ratings (replications) in which the element participates, so long as the rating context is on target (not excessively "easy" or "hard"). The lower portion of the nomograph shown overleaf (in the printed text) illustrates this. In the Rasch method, it makes no difference to the increase in measure precision whether extra ratings result from more raters or more items.

Second, the statistical aspects of the D-Study are trivial. For any average standard error across measures and putative "true" standard deviation of the measures, the reliability can be read directly from the top half of the nomograph. The separation (shown below or to the right of the reliability) is the ratio of "true" S.D. to average S.E. and indicates how many distinct measurement levels the test design can discriminate in this measure distribution.

In practice, target groups of reasonably homogeneous examinees tend to have "true" S.D.'s of 1-2 logits. So, with no data collection at all, one can see immediately the best reliability that any data collection design can yield. Alternatively, one can read off the nomograph how many ratings of each examinee must be collected to reach the desired reliability level.

This nomograph is based on a test targeted on the persons and an effective rating scale. Perverse measure distributions or a poorly functioning scale lessen test precision and can double S.E. size. If some examinees are rated more often than others, or items have different rating scales, use average values.

Example 1: We plan to use 30 item MCQ tests with our 5th grade children. What reliability can we expect?
Answer: Look at the bottom of the nomograph. The precision of a 30 dichotomy test is about 0.5 logits. Our 5th grade children are likely to be fairly homogeneous, with S.D. about 1 logit. Read up from S.E. of 0.5 logits, across from S.D. of 1 logit, to the diagonal line. This line is marked with a reliability of 0.8 and separation of 2. That is the best that we can expect from this design.

Example 2: How many ratings per examinee on a 5 category scale (0-4) is the minimum required if we seek a reliability of 0.85, when previous experience indicates the ability S.D. is 1.5 logits?
Answer: Read across from S.D. of 1.5 logits to the 0.85 reliability line. Then read down. The required average S.E. is 0.6 logits. Read down to the 5 category scale. At least 5 ratings for each examinee are needed.

Example 3: According to the test publisher, an observation protocol has a reliability of 0.66 with four ratings per examinee. How many ratings must be made for a reliability of 0.8?
Answer: Start with the 4 ratings per examinee. Values for S.E. and S.D. are not needed. Simply read up from any "4" in the bottom half of the nomograph, say on the "Dichotomy" line, to reliability 0.66, midway between the 0.6 and 0.7 diagonal reliability lines. Read left to the 0.8 diagonal reliability line. Then read down to the answer on the "4" (Dichotomy) line. At least 9 ratings are needed.

Technical note: The nomograph was constructed using a spreadsheet and standard reliability formulas.
The top section is always the same, regardless of the analysis. It is a graphical representation of the basic reliability relationship:
Reliability = true variance / observed variance = true variance / (true variance+error variance) = true sd² / (true sd² + se²)
The bottom section pictures the estimation of the S.E. This varies somewhat depending on test targeting and the internal structure of the rating scales. To compute it, estimate the average information in a response (e.g., from a response-level residual file or from Rasch theory), and then
S.E. = 1/sqrt (response information * count of responses)

For dichotomies,
T = True S.D. (y-axis in nomograph)
E = Average person S.E. (x-axis in nomograph)
Reliability = True Variance/Observed Variance = T*T / (T*T + E*E)
Then, with reasonable person-item targeting (person ability about 1 logit higher than an item difficulty):
E = 1 / sqrt ( 0.8 * 0.2 * L) where L = number of items in the test
or, if observational data are available,
E = 1/sqrt( the sum of the "Model variance of the observed values around the expected" for the observations of interest).
 
Example: for a sample of persons measured with 30 items:
True S.D. = 1 logit
E = 1 / sqrt ( 0.8 * 0.2 * 30) = 0.47 logits
Reliability = 1*1 / (1*1 + 0.47*0.47) = 1/1.22 = 0.82

Linacre JM. (1993) Rasch-based Generalizability Theory. Rasch Measurement Transactions, 7:1, p. 283-284.

Shavelson RM & Webb NM (1991) Generalizability Theory. Newbury Park CA: Sage.

Rasch-based generalizability theory: Reliability and Precision (S.E.) Nomogram. Linacre JM. … Rasch Measurement Transactions, 1993, 7:1 p.283

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt71h.htm

Website: www.rasch.org/rmt/contents.htm