Thinking with Raw Scores

Why not use raw scores? Are they not immediate and real? Are they not the only indisputable "facts"?

But what have we counted? Real objects which, in this "reality", are manifestly not exchangeable, not equal in their contribution to the count. If we count four apples and each take two, it matters whether you get the two large ones or the two small ones. When we count, we assume exchangeability, i.e., equivalence. So even counting raw scores is not good enough. But it is worse because we expect "one more" always to be the same amount, no matter where we begin or end.

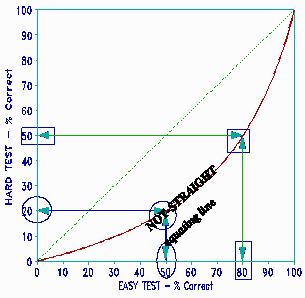
See what happens with raw scores, as shown in the "Equating" Figure overleaf. We expect someone who scores 100% on a hard test to score 100% on an easy test. We also expect someone who scores 0% on an easy test to score 0% on a hard test. What about someone who scores 50% on an easy test? That person must score less, say 20%, on a hard test, or else that test is not harder! Similarly someone who scores 50% on a hard test, must score more, say 80%, on an easy test. So the relationship between raw scores on an easy test and raw scores on a hard test is always the curved, "NOT-STRAIGHT equating line"!

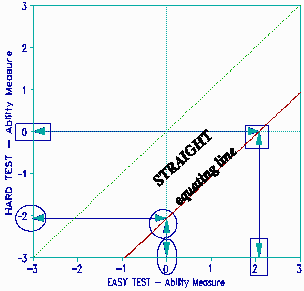
This curvilinear relationship means that it is impossible for one more raw score point, or 1% more correct, to mean the same amount throughout the score range. What we want, of course, is the "STRAIGHT equating line" shown in the "Ability Measure" plot!

One more on a test is not always the same amount. What to do? The scores are the data, but not the desire. How can we make "one more apple" become "one more unit" that is always the same?

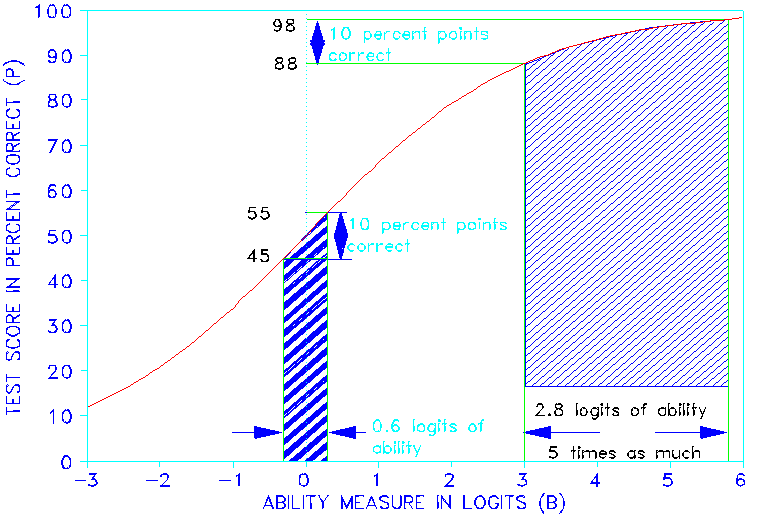
The solution is the Rasch model. This model straightens out the "NOT-STRAIGHT" line into the "STRAIGHT" line by means of a logistic ogive illustrated in the plot of "TEST SCORE" on "ABILITY MEASURE". Notice how a 10% raw score interval near 100% success covers 5 times the ability range of a 10% raw score interval around 50% success. One more score point near an extreme is worth much more than one more score point near the middle. This is why the raw score equating line is curved! Raw scores may be "facts", but facts are not enough, we want what they mean! We need the Rasch model to extract meaning from facts.

Benjamin D. Wright

Equating a Hard and Easy Test
Test Score in Percent Correct	Ability Measure in Logits
{ Test curve is B = 1.5 loge [P/(100-P)] }

Thinking with raw scores. Wright BD. … 1993, 7:2 p.299-300

Thinking with raw scores. Wright BD. … Rasch Measurement Transactions, 1993, 1993, 7:2 p.299-300

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt72r.htm

Website: www.rasch.org/rmt/contents.htm