Rasch Measurement and IEA Studies

Recent advances in statistical methods and supporting software have introduced data analysis possibilities not available to early IEA [International Association for the Evaluation of Educational Assessment] studies. Methods such as multilevel modelling, linear structural equating modelling and item response modelling offer powerful approaches to interrogating IEA data and have the potential to provide deeper insights into factors underlying achievement in different countries.

Among the statistical tools to have become more accessible to educational researchers in recent years is the family of "item response models" now used routinely in national and statewide assessments in a number of IEA countries. Applications of item responses models in IEA research include John Keeves' comparison of international performances on the First and Second Science Studies and Warwick Elley's report of the Reading Literacy Study.

One of the most widely used item response models was developed by Danish mathematician Georg Rasch (1901-1980). Over the past three decades Rasch's model has been studied and applied by researchers throughout the world, but particularly by Benjamin Wright in Chicago, Gerhard Fischer in Vienna, and researchers in the Netherlands and Australia.

The question that led Rasch to his model is a fundamental question in IEA research: Under what conditions is it possible to compare performances across tests or to compare performances on the same test by different groups of students? Rasch was interested in comparing performances on different Danish reading tests over time. IEA researchers are interested in comparing performances not only on different tests over time, but also on the same test across countries and translated into different languages.

Rasch's model provides a framework for addressing these questions. When meaningful comparisons are possible, the model provides a basis for comparing and interpreting test performances across groups, over time, and from instrument to instrument.

A Model for Measuring

It is sometimes assumed that a well-constructed set of test questions will necessarily provide directly comparable test scores. Rasch's model challenges this. Rasch recognized that scores on a test can be compared meaningfully only if the test functions in the same way for all the students tested. If a test functions differently for different student groups, perhaps because of differences in experienced curricula, then comparisons across those groups may not be valid.

Rasch's model draws a distinction between a mere collection of test questions and a measuring instrument. If a set of questions is to function as a measuring instrument, the questions must:
* work together as indicators of the same achievement dimension;
* support the construction of a measurement scale with a defined unit;
* be capable of "calibration" on to this scale so that performances on different selections of questions can be compared directly; and
* function consistently across students answering them.

In other words, to provide the basis for a measuring instrument, a set of questions must satisfy quality control requirements more rigorous than the rules of good test construction and the requirement that they be administered under common conditions. Their behavior must be supervised by an explicit psychometric model and students' responses must be checked continuously for consistency with this model.

Under the supervisory model proposed by Rasch, the probability of a student n correctly answering a particular question i depends on the student's level of achievement β_n in the area being tested and the subject-matter difficulty δ_i1 of that question: ln(P_ni1 /P_ni0 ) = β_n - δ_i1, where P_ni0 is student n's modelled probability of scoring 0 on question i and P_ni1 is student n's probability of scoring 1. Rasch's model for 0/1 scoring can be generalized to questions with several possible scores (0/1/2,...m): ln(P_nix /P_ni(x-1) ) = β_n - δ_ix to provide the "partial credit" form of the model (a name first suggested by IEA psychometrician Bruce Choppin) developed by Masters (1982).

Enhanced Flexibility

Rasch's model can be thought of as specifying conditions which, if satisfied by a set of test data, allow measures of student achievement to be compared directly across tests. When data conform to the model it is possible to use different, overlapping sets of questions with different groups of students, and to delete questions which are problematic in some tests while retaining them in others, without compromising the comparability of student achievement measures.

These possibilities can be useful in IEA studies. Provided that test data approximate the model, it is not necessary for all students to answer the same questions. A bank of calibrated questions can be assembled and different test forms constructed from the bank, even allowing countries choice in the questions they use. Where printing errors or problems of translation arise, individual questions can be set aside in the analysis of data from a particular country while continuing their use in other countries. Rasch's model offers great flexibility in test construction and improved sensitivity to local conditions and testing arrangements. The only cost of these benefits is vigilance in checking that students' responses approximate the model.

Interpreting Achievement Measures

Rasch's model also enables the development of more informative reports of student achievements. Because questions are calibrated and students are measured on the same scale, achievement measures can be interpreted by summarizing the questions calibrated at various positions along that scale to describe the knowledge and skill typically associated with particular test scores. Such interpretations are used routinely in the New South Wales Basic Skills Tests.

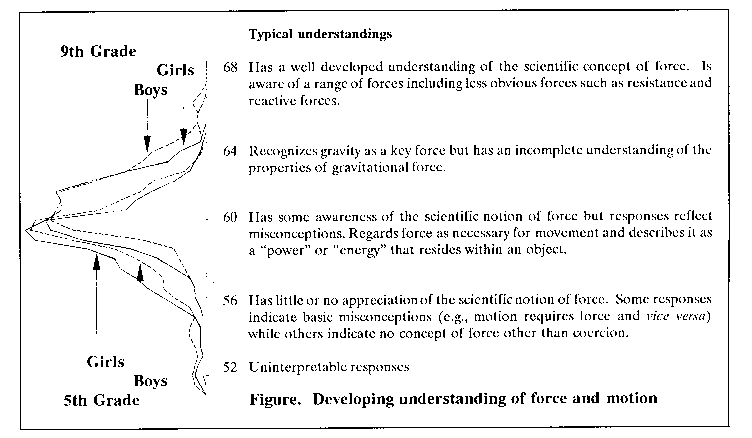
The descriptive interpretation of student achievement levels is illustrated in the Figure. The data analyzed are from a statewide survey of fifth and ninth graders' understanding of science. Students responded to open-ended questions about force and motion. Their responses were analyzed by the Rasch partial credit model. This analysis provided the measures of understanding plotted in the Figure. Each of the force and motion questions was also calibrated on the continuum and used to develop descriptions of typical understandings at various levels of achievement (see text to right of Figure). These descriptions are used to interpret students' test scores.

A similar approach could be used to construct and describe the measurement scales in IEA studies. The advantages will be a better understanding of the measurement scales used in IEA research and reports that are more informative than test scores alone.

Geoff N. Masters
Australian Council for Educational Research

Adapted, with permission, from IEA Bulletin, Vol. 2 No. 2, July 1993. Copyright © IEA 1993.

Rasch measurement and IEA studies. Masters GN. Rasch Measurement Transactions 1993 7:3 p.310

Rasch measurement and IEA studies. Masters GN. … Rasch Measurement Transactions, 1993, 7:3 p.310

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt73c.htm

Website: www.rasch.org/rmt/contents.htm