How to Set Standards

We cannot set a standard unless we decide what we want. We must set up a line of increase, a variable that operationalizes what we are looking for:

This variable is usually brought to life by a test. Then it is the calibrations of the test's items which define the line, and help us to decide how much is "enough". The measures of the test-takers show us who is "more" and who is "less". Making pass/fail decisions requires comparing two points on our line. One point is the measure of the student. The other is our standard. If the test is intended to stratify the test-takers, then many standards may need to be set. [Another attempt at objective standard setting is the Lewis, Mitzel, Green (1996) Bookmark standard-setting procedure.]

The first decision in placing the standard is to locate a criterion point. What point on the arithmetic variable marks out enough "addition"? This requires the qualitative judgment of content experts.

The second decision is to decide on a mastery level. What rate of success on "addition" items is expected? A mastery level of 100% success implies perfect arithmetic ability - an impossibility. 50% success would be at the criterion point. 75% success, 1.1 logits above it. 90% success, 2.2 logits up. Again qualitative judgement is required, guided by the purpose of the test. The criterion point and the mastery level together define the standard.

The locations of person measures and standards are inevitably uncertain:

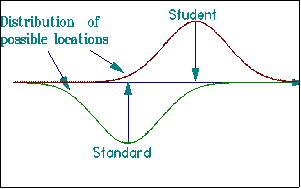
The best we can do is to estimate them with some amount of precision. We can use the normal distribution to qualify our decisions. If we locate a boundary 1.6 standard errors below a student's point estimate, we leave above us 95% of the reasonable-to-expect locations of the student's uncertain position. To put this way of dealing with uncertainty into practice we bracket each point estimate of a measure by ±1.6 Standard Errors:

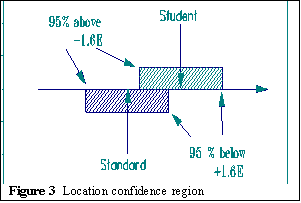
This marks the end points at which we can have 95% confidence in decisions in one direction or the other. Similarly for the standard.

As long as the student region and the standard region do not overlap, a pass/fail decision is clear. When they do overlap, there is a natural asymmetry. When we certify competence, our call is to guarantee quality. We need to be confident only that the student is above the standard. Otherwise the student does not pass:

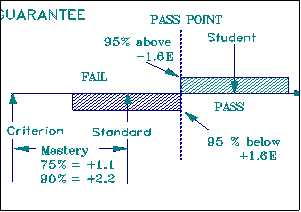
When we certify incompetence, our call is to protect innocence. We need to be confident only that the student is below the standard. Otherwise the student does not fail:

Choosing the Standard Point

Our choice of standard is always a qualitative decision. No measuring system can decide for us at what point "short" becomes "tall". Expert judgment is required. Martin Grosse put into operation a straightforward method at the National Board of Medical Examiners that respects the expertise of judges, while maintaining the quantitative framework of the variable.

The judges are shown item text of calibrated items [see A], but not the calibrations. The calibrations need not be exact - pilot calibrations are good enough. Each judge independently selects items that a minimally qualified candidate should know. Judges can select as many or as few items as they please.

Each judge's item selections are positioned on the variable according to their calibrated difficulties [see B]. A "50% success" criterion is near the center of each judge's selections. An 80% mastery level would be 1.4 logits above this point. This level, applied to each judge's criterion, defines a region in which it is the judges' responsibility to set the final standard. The spread of the judges' own standard points shows the precision of their final standard. Pass-fail decisions based on this standard need to take into account both its uncertainty and the imprecision in test-takers' measures.

You must decide about your cut-point:
1. "I want to pass only people who have definitely passed"
Actual cutpoint = desired cut-point + 1.65*(joint SE)

2. "I want to fail only people who have definitely failed"
Actual cutpoint = desired cut-point - 1.65*(joint SE)

3. "I don't know what I want"
Actual cutpoint = desired cut-point

The utility of this standard is verified by applying it to candidate ability measures [see C]. Do the clearly incompetent fail? Do the clearly competent succeed? Is the failure rate reasonable?

This standard setting procedure produces explicable standards while imposing on judges a minimum of perplexing decisions.

Choosing a Standard

A. The Database of Test Items:

   D = calibrated items
                                 STANDARD
                          D      !
                        D DD     !
                       DD DDD    !
                D  D   DD DDD  D !
                D  DD DDDDDDD  D D
            D   D  DDDDDDDDDDDDDDD    D
     D   D DD DDDDDDDDDDDDDDDDDDDDD D DDD   D  D
D   DDD  D DDDDDDDDDDDDDDDDDDDDDDDDDD DDDD  D DD
0---+---1---+---2---+---3---+---4---+---5---+---
 Easy                            !    Difficult

B. Judges' Criterion Item Selections:

                             :   !
         * *                *:   !
      *  * * *  * *  * * ** *:*  !
0---+---1---+---2---+---3---+---4---+---5---+---
 Easy                        :        Difficult
                   Judge 1's Standard

                           *     !  :
         * ** *****    ****** * *!  :
    *    * ** ****** ************! ** *
0---+---1---+---2---+---3---+---4---+---5---+---
 Easy                               : Difficult
                          Judge 2's Standard

                                 !:
     *                *          !:
*    *              **** ****    !:**
0---+---1---+---2---+---3---+---4---+---5---+---
 Easy                             :   Difficult
                        Judge 3's Standard

                        * *      ! :
               *****  ******** **! :
              *******************! :  *
0---+---1---+---2---+---3---+---4---+---5---+---
 Easy                              :  Difficult
                         Judge 4's Standard

C. Candidate Performances:

                                 !  R
                                 ! RR
                  FAIL           !RRRR     PASS
                                 RRRRRRRR
                                RRRRRRRRRR
                               RRRRRRRRRRRRR
         R          R  R    RRRRRRRRRRRRRRRRRR R
0---+---1---+---2---+---3---+---4---+---5---+---
 Less Able                       !    More Able
                                 STANDARD

Ben Wright & Martin Grosse

How to set standards. Wright BD, Grosse M. Rasch Measurement Transactions 1993 7:3 p.315

Relevant references:
Grosse, M.E. & Wright, B.D. (1986) Setting, evaluating, and maintaining certification standards with the Rasch model. Evaluation and the Health Professions, 9, 267-285.
Wang, N. (2003). Use of the Rasch IRT model in standard setting: An item mapping method. Journal of Educational Measurement 40(3), 231-253.

How to set standards. Wright BD, Grosse M. … Rasch Measurement Transactions, 1993, 7:3 p.315

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt73e.htm

Website: www.rasch.org/rmt/contents.htm