Making Raw Score Summaries Usefully Linear

Research is often reported as means and standard deviations of raw scores, percents or ratings. These scores compress towards the ends of their scale due to their finite range. Since log-odds extend to infinity in both directions, a simple log-odds transformation can remedy the compression problem.

Here is the transformation, when raw score means are available:

"Mean measure" is the linearized mean measure, relative to the center of the raw score scale. "Mean" is the reported mean raw score. "Bottom" is the lowest raw score possible. "Top" is the highest raw score possible.

Hagemann (1994) reports that teachers rate children's reading with an average raw score of 2.85. The raw score range was 1, "inadequate" at the bottom, to 4, "above average" at the top.

Then

When a mean score, "m", and a standard deviation, "s", are reported, a better linearization is:

"b" is the lowest raw score possible. "t" is the highest raw score possible.

The linearized standard deviation around this mean measure is

In Hagemann, the raw score standard deviation is .80, so a better mean measure is:

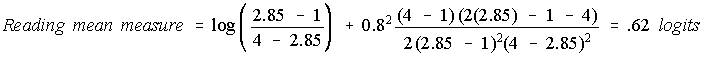
with measure standard deviation

Stuart Luppescu 1994 RMT 8:1 p. 337

Hagemann M (1994) Interpreting teachers ratings requires caution. Paper presented at MOMS, May 1994.

Making raw score summaries usefully linear Luppescu S.. … Rasch Measurement Transactions, 1994, 8:1 p.337

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt81d.htm

Website: www.rasch.org/rmt/contents.htm