From Percent-correct-values, P-values, and Raw Score Statistics to Logits

Conventional statistics and examinee raw scores may be all that remain of the data from a previous testing. These statistics provide the mean of the N examinee raw scores, their standard deviation and, for each item i, the rate of success of the sample of examinees, a percent-correct-value, "p-value", P_i, for i = 1 to L items.

In order to equate examinee performances on this earlier test with those on other tests, or to add these earlier items to an item bank, conversion from the raw score metric to a linear metric is needed. This can be achieved with a simple, usefully accurate technique, provided that it is reasonable to think of the examinees as randomly selected from a normal distribution.

Here's how to construct logit measures from raw score statistics:

1. Check the raw score statistics for consistency:

Is the examinee mean raw score

?

Are there typographical errors?

Even if p-values were obtained from one sample and mean examinee score from another, they may still be close enough for this computation.

Adjust for the spread of person abilities in the sample ...

2. Compute a raw score-to-ability conversion factor, C_b:

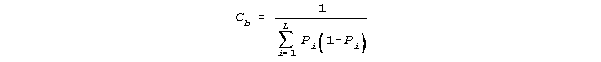
3. Compute a logit examinee ability variance from SD, the examinee raw score standard deviation:

4. Obtain an item calibration expansion factor, X_f, to adjust item difficulties for examinee ability variance:

Estimate the item difficulties ...

5. Compute a logit difficulty calibration for each item, d_i:

6. The standard error, SE_i, of calibration d_i for item i is:

Build a score-to-measure table for the test ...

7. Compute an initial logit ability estimate br^o corresponding to each raw score r from 1 to L-1:

8. Compute a final ability estimate br corresponding to each raw score r from 1 to L-1 by iterating the equation:

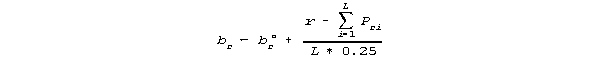
where

replacing b_r^o by b_r and recomputing, until

9. For examinees with extreme scores of 0, compute b₀ using steps 7 and 8 with r = 0.25.

10. For examinees with extreme scores of L, compute b_L using steps 7 and 8 with r = L - 0.25.

11. The standard error, SE_r, of person ability measure b_r, corresponding to raw score r, including r = 0.25 and r = L - .25, is:

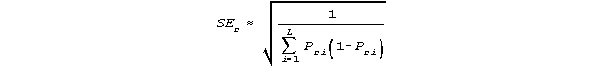
This algorithm has been applied successfully to empirical data.

A. J. Stenner, B. D. Wright & J. M. Linacre 1994 RMT 8:1 p. 338

From P-values and raw score statistics to logits. Stenner AJ., Wright BD., Linacre JM. … Rasch Measurement Transactions, 1994, 8:1 p.338

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt81e.htm

Website: www.rasch.org/rmt/contents.htm