What Does Generalizability Theory (G-Theory) Offer that Many-Facet Rasch Measurement Cannot Duplicate?

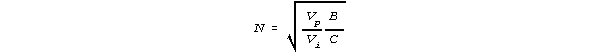
"A major contribution of G-theory is that it permits a decision maker to pinpoint the sources of measurement error and change the appropriate number of observations accordingly in order to obtain a certain level of generalizability" (Marcoulides 1993 p. 197).

Sources of measurement error are identified and quantified in a Generalizability Study (G-study). Decisions are then made concerning which of these sources are small enough to be ignored or, better, which sources permit a reduction in the number of relevant observations in the subsequent Decision Study (D-study) without significantly reducing the generalizability coefficient (i.e., reliability).

Since resources are invariably limited, such information could be helpful in evaluating how best to employ those resources. Marcoulides points out that these decisions have often focussed on reliability and measurement error exclusively, ignoring sampling error and sample size considerations. He suggests how both types of error can be addressed simultaneously in meeting budget constraints.

Consider a Marcoulides' formula. It suggests a simple solution to a typical design problem. When one wants to minimize error variance for a paper-and-pencil test of L items, administered to N subjects, with cost-per-response of C and a budget of B, then N and L are given by

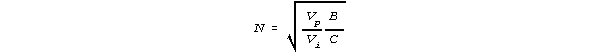
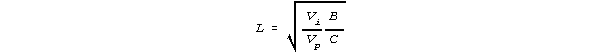
where V_p is the "true" variance of the person responses across items, and V_i is the "true" variance of the item responses across persons, and V_i and V_p are estimated during the G-study. How well these values of V_i and V_p will carry forward to the D-study, however, is never determined.

In Many-facet Rasch Measurement (MFRM), a preliminary study, i.e., a G-study, is not necessary. When the items are reasonably targeted on the persons, measurement error can be estimated from theory, e.g., via a nomograph (RMT 1991 7:3 283). The measure variance of the subjects and test items is usually well enough known from experience. If an earlier data analysis of similar data is available, the results of that analysis can be used.

In MFRM, Marcoulides' formula carries forward directly. The algebraic form is identical, but now V_p is the adjusted, i.e., "true", person measure variance, and V_i is the adjusted, i.e., "true", item measure variance.

MFRM, however, goes beyond G-theory in providing a comprehensive framework for test design. G-theory starts just before the first data collection, the G-study. MFRM starts with the first conceptualization of the testing problem. What is the variable on which measurements are to be obtained? How is this variable to be expressed in terms of an ascending sequence of test items? How is the rating scale to be defined to accord harmoniously and unambiguously with the variable definition?

G-theory stops before the main data collection starts. At this point all error terms have been quantified, and will be asserted to maintain their values during the ensuing data collection. MFRM continues until the test reports have been written, and will continue to influence the readers as long as they maintain interest in that measurement variable. In particular, MFRM continues to estimate measure variances and measurement error throughout the data analysis. It also evaluates and reports data quality (fit), identifying items and persons with performances meriting special attention, perhaps remediation, perhaps even omission from the current analysis. When data analysis starts while data collection is still underway, MFRM monitors data and judging plan quality.

There is, however, yet a further fundamental issue raised by differences between MFRM and G-theory. The ultimate goal of G-theory is "reliable" measures, generally expressed in the reproducibility of raw scores. There is a point, however, at which such raw score reliability is achieved at the expense of validity (See Engelhard, RMT 6:4 257 on the attenuation paradox). This is particularly true in the case of judge-mediated examinations in which almost all the recommendations on how to achieve "reliable scores" involve restricting how judges grade, and/or atomizing the tested behavior into some form of unrecognizable check list.

In MFRM, although the statistical bases for reliable measures are still present, the emphasis shifts to the reproducibility of measures of a students' ability. These measures are freed from the particular items used to elicit this performance and the particular judges that rated the performance, so reproducibility of raw scores is of little importance. Even measure reproducibility is seen to have its limits. No student (or item, or judge) functions consistently at exactly the same level of performance throughout the entire testing experience. Consequently, the endeavor to estimate measures with pin-point precision is futile. Usefully stable measures are the best that can be hoped for, and, in fact, all that is needed.

By focusing on the reproducibility of the latent trait rather than forcing judges to generate the same raw score, the concept of reliability takes its rightful place in supporting validity rather than being in tension with it. This I consider to be the crucial point that differentiates MFRM from G-Theory.

John A. Stahl

Marcoulides, George A. 1993. Maximizing Power in Generalizability Studies Under Budget Constraints, Journal of Educational Statistics, 18:2 197-206.

See also:
"Generalizability Theory" in Facets Help
"Construction of Measures from Many-facet Data" pp.495ff. John M. Linacre. Benjamin D. Wright. Journal of Applied Measurement (2002) 3(4), 484-509.

What Does Generalizability Theory (G-Theory) offer that Many-Facet Rasch Measurement cannot duplicate? Stahl JA. … Rasch Measurement Transactions, 1994, 8:1 p.342-3

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt81j.htm

Website: www.rasch.org/rmt/contents.htm