Rasch Factor Analysis

Conventional Factor Analysis input x_ni is a test score, Likert rating or MCQ response of person n to item i. Incommensurable origins and scales are reconciled by using sample means and standard deviations to commensurate items:

(1)

This "equating" depends on complete data. When data are missing, they must be feigned or incomplete persons or items deleted. The model for Factor 1 is:

(2)

{u_n1} n=1,N is a vector of person "factor scores"
{v_i1} i=1,L is a vector of item "factor loadings"

The Factor 1 residual is:

(3)

Whether this residual is all error or contains other factors is unknown. To find out, the residual is taken as the data for Factor 2. Matrices of decreasing residuals {{z_nij}} j=2,M are extracted in turn to calculate the M factor model:

(4)

Optimal values for person and item vectors {u_nj} and {v_ij} for each Factor j in turn are found by minimizing:

(5)

Decomposition to identify each Factor j is done by initializing at w_nj=1 and iterating equations:

	(6)

until changes in {w_nj} become uninteresting.

Factor score w_nj is the value predicted by Factor j's regression on "independent" variables i = 1,L with regression coefficients {v_ij}.

Problems with Factor Analysis of Observational Data:

1. Since, data {{x_ni}} are never linear measures, Equations (2) and (3) cannot work in a reproducible way.

2. The necessity for complete data is awkward.

3. The residuals {{z_nij}} for seeking smaller factors are awash in turbulence left by preceding larger factors.

4. There is no way to know when to stop factoring.

5. Few algorithms provide standard errors for factor loadings or factor scores.

6. When old items are refactored from new data, factor sizes, loadings and number of factors change.

Most factor analysts can tolerate problems 1-5. Problem 6, however, is impossible to swallow. As analysts notice the numerical fragility of their structures, they abandon their person factor scores and ignore everything in the factor loadings except which factor gives each item its highest loading.

Person scores for these "same factor" clusters are obtained, not from factor scores, but by summing the standardized person responses z_ni1 to the clustered items.

Rasch Factor Analysis:

Since data {{x_ni}} are labels for ordinally interpreted qualities, we address them with a probability model for ordered categories. For a dichotomy, we recognize x_ni=0,1 as a binomial. The error model which follows is not the ill-chosen linear error model of factor analysis, but a binomial probability P_nix for the occurrence of x_ni:

(7)

from which

Parameters, as with factor analysis (5), can be estimated by minimizing:

(8)

but now we get, not only least-square (maximum likelihood) estimates of linear person measures B_n and linear item calibrations D_i on their common variable, but also a stochastic basis, the binomial error variances pni1pni0, for estimating useful standard errors and evaluating the probabilities of residuals:

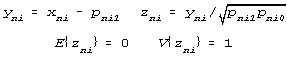(9)

This enables detailed misfit analysis which, in turn, allows a partition of the matrix of residuals {{z_ni1}} into those many z_ni1 which are observed to be no greater than the probability model expects, say |z_ni1| < 2, and the subset of more extreme residuals, say |z_ni1| > 2 or 3, which are sufficiently improbable to invite investigation.

It is only when improbable residuals emerge that there is an incentive to look for a second variable. The improbable residuals tell us where to look. Should there be another useful variable in these data, it will be most evident among the responses to the subset of items and persons which misfit the first analysis.

To seek a second variable, therefore, we apply the probability model again, not to the whole matrix of residuals {{z_ni1}}, but only to the original ordinal responses {{x_ni}} to this subset of items. We estimate a new set of linear item calibrations {D_i2} for these items, along with a new set of additive conjoint person measures {B_n2} on this newly defined "Variable 2". To find out whether Variable 2 is useful, we plot person measures {B_n2} against person measures {B_n1}. This plot will show us the extent to which we have found a useful second variable.

Benjamin D. Wright 1994 RMT 8:1 p. 348-9

Rasch factor analysis Wright BD. … Rasch Measurement Transactions, 1994, 8:1 p.348-9

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt81q.htm

Website: www.rasch.org/rmt/contents.htm