Predicting Item Difficulties from item characteristics

Raven's (1986) progressive matrices are used to measure non-verbal intelligence: the capacity to reason by analogy, form comparisons, and think logically. The Coloured Progressive Matrices (CPM) is the 36- item version of the test used with children ages 5-12.

The complex and visual CPM items are not well understood, so we identified 14 characteristics that we thought might differentiate item difficulty (see Table 1, and Green and Kluever, 1992). Each CPM item was rated on each characteristic. Each characteristic was modelled to have its own rating scale. The 14 characteristics were then treated as agents and the 36 CPM items as objects in a Rasch analysis. The purpose of this analysis was to construct a conceptual difficulty for each CPM item based on the number and complexity of its characteristics.

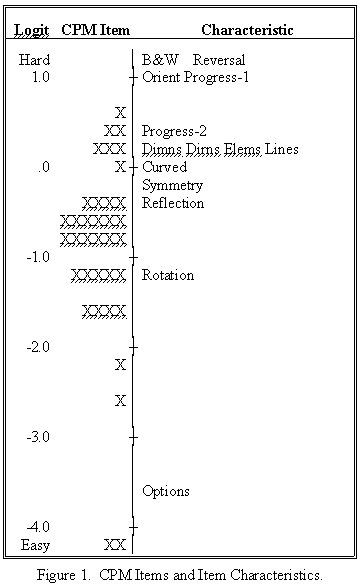
Figure 1 shows the measures of characteristics and items. CPM items with high measures exhibited many characteristics. Characteristics with high measures were exhibited by few CPM items. Reversal (background to foreground) and B&W (colors limited to black and white) were the least observed characteristics. Only the simplest CPM items have less than 6 response Options.

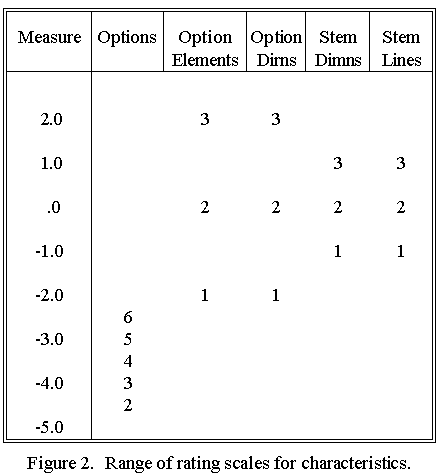
Figure 2 shows a map of the ratings associated with each characteristic. According to this map, a change in the number of lines and dimensions in the stem indicates less of a change in overall CPM item complexity than a change in number of elements or number of directions in the options.

To see how well these conceptual difficulty measures capture the empirical difficulties of the CPM items, the 36 CPM items were calibrated for 2 samples. The first sample was 457 1st through 5th grade children from rural southern Colorado. The second sample was 268 relatively gifted 4 through 12-year old children at an educational assessment center at the University of Denver. The results for the two samples were reassuringly similar.

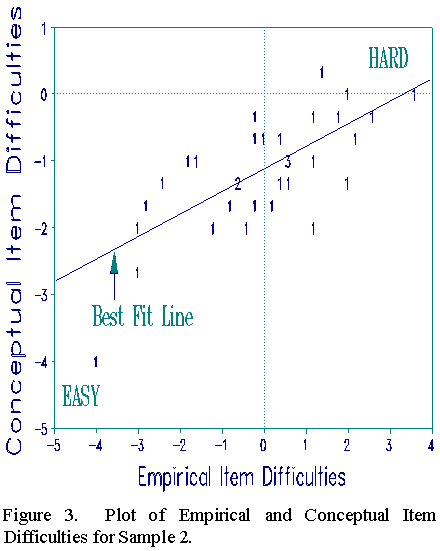
After elimination of 4 CPM items as too easy or markedly misfitting, Figure 3 shows the plot of 32 conceptual item difficulties against empirically derived ones for sample 2. The correlation is .66. This implies that, after correcting for measurement error, our initial set of 14 characteristics has already explained about half the variance in item difficulties

A commonly used alternative approach to item difficulty decomposition is to regress the empirical item difficulties on the characteristics. But the item characteristics are multicollinear, so regression results are heavily influenced by the CPM-item-dependent variances in the characteristic ratings. If the characteristic rating variances were to change, even slightly (e.g., by omitting a CPM item), a different characteristic would take precedence in the regression analysis. This perplexes the researcher.

The Rasch approach, however, goes beyond multiple regression by clearly ordering the item characteristics according to their complexity. The level of successful prediction of empirical difficulties suggests that continued development of this set of item characteristics will be fruitful. The item maps provide the clarity needed to advance thought about identified and potential item characteristics and the general nature of CPM item difficulty.

Green KE & Kluever RC (1992) Components of item difficulty of Raven's Matrices. Journal of General Psychology, 119, 189-199.

Raven JC, Court JH & Raven J (1986). Coloured Progressive Matrices. London: H. K. Lewis & Co.

Predicting item difficulties from item characteristics. Green KE, Kluever RC, Wright BD. … Rasch Measurement Transactions, 1994, 8:2 p.354

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt82c.htm

Website: www.rasch.org/rmt/contents.htm