Clinical Diagnosis by Likelihood Triangle

Differing medical conditions often exhibit similar symptoms. Rasch measures can assist clinicians by portraying the relative likelihoods of diagnoses based on observed symptom severity.

Suppose three types of injury produce similar symptoms but with different intensities. Samples of patients identified to have each type of injury are used to calibrate the symptoms on the relevant variable of injury severity. This defines three variables, gives each symptom three calibrations, and produces three raw-score-to-measure tables, one for each diagnosis.

When a new patient comes in for diagnosis, a rating of the severity of each symptom is recorded. The sum of these ratings, the patient's raw score, produces three measures, (Bj, Bk and Bl), one for each of the diagnoses, j, k, and l.

From these measures, the likelihood of the observed pattern of symptom severities is estimated for each diagnosis.

Diagj = Prod(Pji(Xi)), for i=1 to L, is the likelihood of diagnosis j. Pji(Xi) is the usual Rasch probability of the patient's observed severity level Xi, on symptom i for diagnosis j, when the patient's overall measure is Bj.

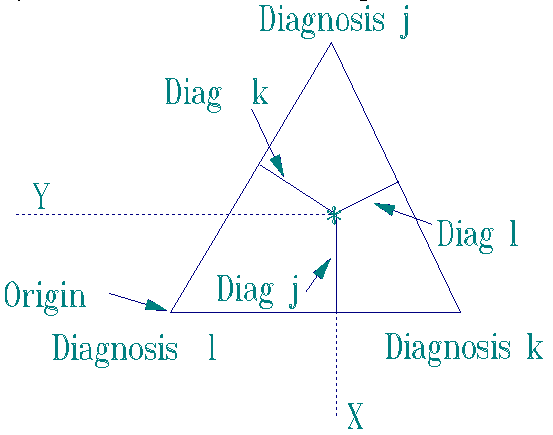
The likelihood of each diagnosis is plotted to locate the patient among the diagnoses. The plot is an equilateral triangle, in which the distance from the side opposite the diagnostic vertex is proportional to the likelihood of that diagnosis. This locates the profile of symptom severities in the plane of the three diagnoses, nearer the more likely diagnoses.

The vertices of the equilateral triangle, the locations of the diagnoses, are at (0,0) for diagnosis l, (m,0) for diagnosis k, and (m/2, msqrt((3/4)) for diagnosis j, where m is a chosen to give a conveniently sized triangle. The location of the central profile point, *, is ( m(Diagk + Diagj/2)/(Diagj + Diagk + Diagl), mDiagj(sqrt((3/4))/(Diagj + Diagk + Diagl) ).

If diagnosis j is most probable, with likelihood 0.3, and diagnosis k is 0.2, diagnosis l is a least probable 0.1, the vertices are at (0,0) (1,0) and (0.5, 0.87) when m=1. The profile location is (0.58, 0.43). This shows a location nearer j than k and far from l, enabling the clinician to select at a glance an efficient screening procedure for identifying the correct diagnosis.

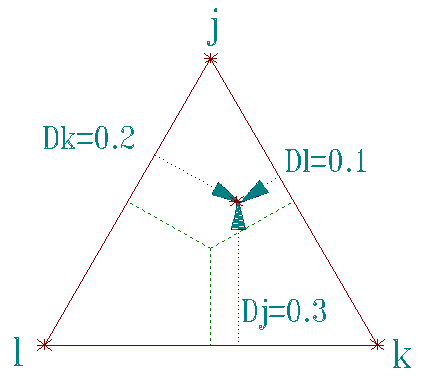
Clinical diagnosis by likelihood triangle. Granger CV. … Rasch Measurement Transactions, 1994, 8:2 p.357

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt82e.htm

Website: www.rasch.org/rmt/contents.htm