Ranks in Sensory Measurement

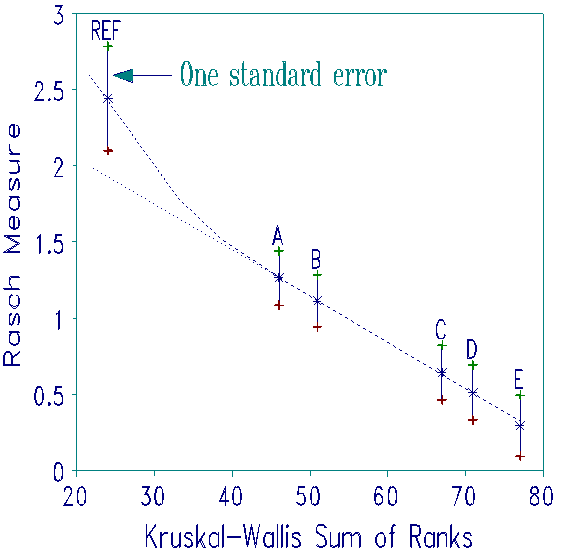
Though rating scales are usually preferred for sensory measurement, rank ordering is often cheaper, faster and easier, particularly when the number of objects ranked is between 5 and 10, and the raters are not highly trained. Ranking also has the advantage of removing the effect of judge severity, while permitting judge ranking patterns to be compared for quality control.

Ranking has its disadvantages. It is difficult to combine data from different rankings, and the information contained in the data is limited. It is also awkward to reanalyze rankings in order to investigate a different hypothesis.

Since few human judges can compare 5 objects simultaneously, the analysis of rank order data has been burdened with the need to model a selection mechanism (e.g., as a series of paired comparisons) into the observation model. In practice, when results depend on the intricacies of an often unconscious ranking procedure, ranking can become too fragile a basis for substantive conclusions.

To check the robustness of ranked results, we compared the location statistic used by Kruskal-Wallis (K-W) and a many-facet Rasch procedure. K-W uses the sum of the ranks given to an object as the basic statistic, and tests for global differences with sigma**2. The many-facet Rasch procedure models the ranks as qualitatively-ordered categories which have one observation per category per ranking. A simple Rasch model for complete rankings without ties is

log_e(Pnj/Pn(j-1)) = Bn - Fj j=1,m-1

where Bn is the measure of object n, and Fj is the step measure up from a rank of j+1 to j. A sufficient statistic for Bn is the K-W sum of ranks.

An experiment was conducted in which 5 test materials, A-E, and a standard reference material, REF, were ranked 16 times. The K-W and many-facet results are compared in the plot.

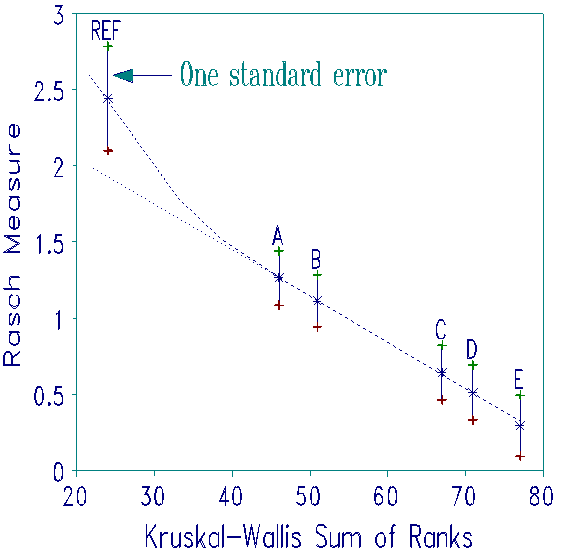
Both methods show the Reference material to be located higher than the test materials. The Rasch method provides standard errors from which we can infer that the Reference material is significantly better than the best test material. The relationship between the Rasch measures and the summed ranks is close to linear with the curvature of the logistic ogive only in evidence for the highly ranked REF material. Nevertheless, this curvature raises the measure of the REF material noticeably - an important consideration when these measures are used in a cost vs. quality analysis.

Rasch, unlike K-W, also provides quality-control fit statistics for the rankings, and consistency statistics for the objects being ordered. Test material A was the most consistently ordered, showing that its placement as the best test material is generally agreed. Test material D was the least consistently ordered. Further investigation may discover something about material D that appeals to certain judges.

Rasch analysis also identifies quirks in the data. The most unexpected observation is a ranking of 4th for the Reference material by one judge. What motivated this idiosyncratic ranking? Does it indicate an opportunity for further improvement?

The similarity of the meaning of the location estimates for K-W and Rasch is reassuring to the practitioner. But Rasch provides additional valuable insight easily overlooked by the harried analyst.

Ranks in sensory measurement. Rehfeldt TK. … Rasch Measurement Transactions, 1994, 8:2 p.368

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt82p.htm

Website: www.rasch.org/rmt/contents.htm