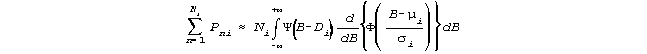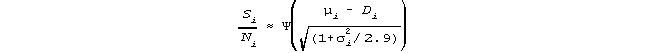PROX with missing data, or known item or person measures

The Normal Approximation Estimation Algorithm (PROX) is a computationally simpler Rasch estimation algorithm invented by Leslie Cohen in 1972 for responses by persons to dichotomous items with no missing data. It has been extended to many-facet polytomous data sets with missing data. The essential specification is that each element (e.g., person, item, task) encounters a symmetrically distributed sample of challenges (e.g., person facing items+tasks+judges). The distributions of challenges faced by the elements may have different means and variances.

Iterative PROX: the theory

For convenience, consider the two-facet case of persons of ability {B_n} facing items of difficulty {D_i}. Then, according to the Rasch model, for each dichotomous encounter there is the logistic relationship

(1)

Sum for each item i across all N_i persons it encounters,

(2)

where S_i is the raw score of successes on item i, and Ψ is the standard logistic function.

When the {B_n} are symmetrically distributed, summing across them can be approximated by integrating across N_i normal distributions of {B} with mean μ_i and standard deviation σ_i for item i:

(3)

where Φ is the normal cumulative distribution function.

An equivalence between logistic Ψ and normal cumulative probability distributions Φ (Camilli 1994) is

(4)

producing,

(5)

But, in general, for the cumulative normal distribution function,

(6)

Then, since 1.702² = 2.9,

(7)

Substituting the logistic for the normal ogive,

(8)

and rearranging, produces an estimation equation for D_i, the logit difficulty of item i,

(9)

where μ_i is the mean and σ_i the standard deviation of the logit abilities of the persons encountering item i.

The comparable estimation equation for person n with logit ability, B_n, is

(10)

where R_n is the raw score achieved by person n on N_n items, and μ_n and σ_n summarize the distribution of logit item difficulties encountered by person n.

The model standard errors of PROX measures follow:

(11)

Iterative PROX: in practice

1. Start with all person and item difficulties set to 0, so that μ_i=0, σ_i=0, mu;_n=0, σ_n=0
2. Compute the item difficulties:

(9)

(10)

(11)

For more than two facets, the {μ_i} and {σ_i} summarize the distribution of the combined measures of the other facets, as encountered by item i, and similarly for the persons, tasks, judges, etc.

PROX for Complete Data

If data are complete, then μ_i and σ_i can be treated as constant across items, and μ_n and σ_n constant across persons. This, with further simplifications, permits the non-iterative estimation equations derived by Cohen (1979):

L = count of items
N = count of persons
S_i is the raw score of successes on item i
S_n is the raw score of successes by person n
SD_L = sample S.D. of item raw scores
SD_N = sample S.D. of person raw scores
 
Item difficulties:
X_L = item difficulty expansion factor = √ [(1+SD_N/2.89)/(1-SD_LSD_N/8.35)]
Provisional difficulty of item i = - X_L*ln[(S_i)/(N-S_i)]
Difficulty of item i = Provisional difficulty of item i - Average provisional difficulty of all items
with S.E. of item i = X_L*√[N /(S_i*(N-S_i))]
 
Person abilities:
X_N = person ability expansion factor = √ [(1+SD_L/2.89)/(1-SD_LSD_N/8.35)]
Ability of person n = 0 + X_N*ln[(S_n)/(L-S_n)]
with S.E. of person n = X_N*√[L /(S_n*(L-S_n))]

PROX estimation equations for polytomous data will be derived in the next RMT.

John Michael Linacre

Camilli, G. 1994. Origin of the scaling constant d=1.7 in item response theory. Journal of Educational and Behavioral Statistics. 19(3) p.293-5.

Cohen, L. 1979. Approximate expressions for parameter estimates in the Rasch model. British Journal of Mathematical and Statistical Psychology 32(1) 113-120.

PROX with missing data, or known item or person measures. Linacre JM. … Rasch Measurement Transactions, 1994, 8:3 p.378

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt83g.htm

Website: www.rasch.org/rmt/contents.htm