Rasch sensitivity and Thurstone insensitivity to graded responses

David Andrich (9-27-94):

Here I explain one major difference between the Thurstone and Rasch models for graded responses. Consider Thurstone's graded response model expressed for convenience in the logistic (rather than normal) form and with the equivalent number of parameters for any item i.

If Y_pi is a random continuous process on the continuum about the location B_p of person p, and if successive categories of item i are denoted by successive integers x_pi {0,1,2,..,m}, then an outcome T_xi < y_pi <= T_(x+1)i leads to the outcome x_pi, with x_pi = 0 if y_pi <= T_1i, and x_pi = m if y_pi > T_mi, where T_xi is a threshold or boundary between categories x_pi and (x+1)_pi.

Define
, then, formally Thurstone's model is

Let
be the cumulative probability from category x_pi to the last category, then Thurstone's model becomes
.

The probability of response in each category x_pi is given by the difference of successive cumulative probabilities

that is,

and

Clearly, the probabilities of two adjacent categories are modeled to be additive in the following sense:

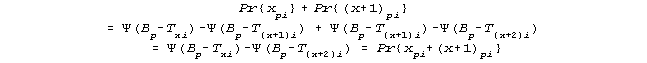
The Rasch model (sometimes called the partial credit model and sometimes the rating scale model when all of the items have the same parameters for the category boundaries), can be written in exponential form, but the log_e odds of being it two adjacent categories x+1 and x, or x+2 and x+1 are respectively given by

These log-odds are modelled to be additive in the following sense:

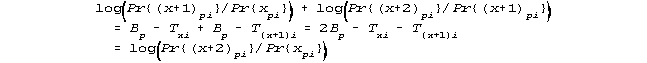
Because the log-odds transformation is a non-linear transformation of the category probabilities, the log-odds and the probabilities themselves in the Rasch model cannot both be additive simultaneously. This is a crucial difference between the Thurstone and Rasch models -- in the former, the probabilities across successive categories are additive, in the latter the log_e odds across pairs of successive categories are additive. The latter also implies that it is the parameters that are additive, but I wish to focus on the major surprising consequence of the above analysis that in the Rasch model, adjacent categories cannot be simply pooled or collapsed. If the data fit the model with say, 5 categories, then they will not fit the model to the same degree with less than 5 categories, including two categories when the data are dichotomized.

Ben Wright (10-8-1994):

Who can disagree with such an exposition? But there is much exploration and trial and terror that precedes any final questions as to which scoring of the response categories is a "most useful" one. That only one scoring can be algebraically "right" can be a useful tool for finding out from a set of data which of the various possible scorings, which seem plausible under the circumstances encountered, works best - in the sense of patterns of fit (and misfit) and person and item separations and most of all meaning and the conjoint structure of item and person hierarchies.

I begin with an observation model which limits what I let a respondent tell me to the few response categories precoded on the data collection device (or postcoded from less well defined data such as interviews, classroom observations). Without further assertion, these data are basically nominal. However, there is almost always a dominant, even when implicit, order for the response categories. We do know a "right" answer from a wrong one, usually.

My second step is to find out how to represent this putative order by trying a scoring model. It usually begins as 0,1,2,3,4,5,,, for the categories in their presumed/intended order. But I know from experience that respondents often do not care enough, or notice enough, to distinguish consistently between my adjacent categories. These respondents use some of my carefully ordered adjacencies as though there were randomly equivalent. When I insist on scoring an order for these undistinguished adjacencies I find I increase the noise in the data. This invites me to simplify my scoring model to specify less distinctions, as in 0,1,1,1,2,2,3,3,3,,,,. Often this kind of rescoring of the response categories produces a more satisfying set of calibrations, measures and fits.

Shall I conclude from my best fit, then, that I have found a "right" way to understand my data? Does your algebra give me that?

David Andrich (10-25-1994):

What you have been doing in collapsing categories when they do not seem to work is exactly what my algebra says you should do. If one has posited 7 categories, but people could only work with 4, say, and you work this out from your diagnostics, then you should collapse the categories accordingly. Because the model is so sensitive to the number of categories, you should work out the number of categories that is really working in the data, and collapse the data into just those the categories.

However, once you have the optimum number of categories for the data expressed through the model, collapsing categories further will be counterproductive. Though surprising in the first instance, this is consistent with the usefulness of collapsing categories when they are not working, If you could collapse categories whether or not they were working, then it would be of no use to collapse them when they were not working - what point would there be to collapse categories if you could do it whether or not they were working? If categorization is to have any meaning, the model must be sensitive to the collapsing of categories.

But this is exactly not the state of the Thurstone model. It does not matter in this model whether or not the categories are collapsed. It is of no benefit in the Thurstone model, if you perceive that the categories are not working, to collapse them -- the model is insensitive to collapsing.

This is all so consistent that it is beautiful! In the first instance, it seems counterintuitive, but in the end it is exactly as it should be.

This is all consistent with what you do now. Once you have discovered that some ordered category system works with, say, 4 categories, you do not collapse further because you would be not only lowering the overall fit, but also losing the precision that is really there. Collapsing categories too far is rejected by the model because the model no longer characterizes the actual precision in the data. This is a telling distinction between the Thurstone and Rasch models.

This insight really does establish that the Thurstone model is not simply an alternative to the Rasch model. The Thurstone model is not suited to the typical situation to which we apply the Rasch model. When this is realized, it will be a shock to the establishment which uses the two models as if the choice is just a matter of taste, or alternatively deceive themselves into thinking that the properties of the Thurstone model make it superior just because it is insensitive to the workings of the categories.

Paradoxically, insensitivity of the Thurstone model aids sloppiness, not utility. One can have the categories working any old way: ordered, multidimensional, discriminating backwards, and so on. The Thurstone model is insensitive to all this! What worth can we then put on the putative order of the categories if the model is happy with anything in the data, order or not?

Ben Wright (11-7-1994):

As you put it so well, The Thurstone and Rasch models disagree as to the status of the categories. In the Thurstone model, the categories are essentially meaningless partitions of the data. In the Rasch model, there is the useful scoring model, the one the respondents conversed in terms of, and neither less nor more will do as well.

But how is the analyst to identify this unique scoring model? My program, BIGSTEPS, dutifully produces many statistics for each category, but my own explorations have centered on 1) the mean ability of each category's users (a very useful indicator as to whether the category ordering is advancing the variable), 2) the observed frequency of each category (which directly relates to the step difficulty), and 3) the pattern of fit across categories. On a global level, I expect that 4) a better scoring model will produce better statistical separation of respondents.

David Andrich
School of Education
Murdoch University
Murdoch WA 6150
Australia

Ben Wright

Rasch sensitivity and Thurstone insensitivity to graded responses. Andrich D, Wright BD. … Rasch Measurement Transactions, 1994, 8:3 p.382

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt83m.htm

Website: www.rasch.org/rmt/contents.htm