Point-Biserial Fit Indices

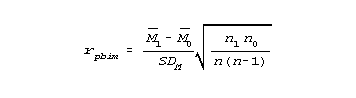
Richardson and Stalnaker (1933) derived rpbis, the point-biserial correlation between an ordinal scale with only two values and a continuous, interval scale, based on the biserial correlation of Karl Pearson (1909). Nowadays, rpbis is often the "corrected" correlation between respondents' right/wrong responses to a target item and their ordinal raw scores on the test (without the target item) (Henrysson). rpbis indicates the extent to which an item cooperates with the rest of the test. It is useful in Rasch analysis because negative values detect miskeyed MCQ responses and negatively worded survey questions. Other diagnostic use, such as detecting redundancy by means of overly high positive values, is problematic because of deficiencies in rpbis.

An obvious improvement in rpbis would be to replace ordinal raw scores by interval ability measures. This produces the point- bimeasure correlation, rpbim:

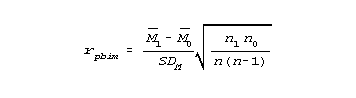
where
M1 is the mean measure of the n1 respondents answering the item correctly
M0 is the mean measure of the n0 respondents answering the item incorrectly
SDM is the standard deviation of all n1+n0=n respondent measures.

Even rpbim, however, is sensitive to targeting. With a uniform distribution of person abilities, the maximum rpbim could be .71 for an item with p-value .95, but .87 for an item with p-value .50. The corresponding minimum values could be -0.71 and -0.87. But ranges need not be symmetrical about 0. Fortunately rpbim's sensitivity to targeting can be reduced by standardizing its range to -1.0 to 1.0.

The maximum rpbim attainable for any item p-value is the one produced by its Guttman pattern (all 1's by high ability respondents, all 0's by low). The minimum rpbim is the anti- Guttman pattern (all 0's by high ability respondents, all 1's by low). This provides a standardized rpbig ("g" for Guttman):

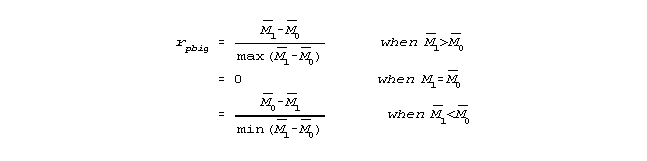
Negative values continue to indicate that this item is "working backwards", contradicting the construct. But values close to 1.0 are now diagnostic. They indicate a local lack of stochasticity in the data.

Jack Stenner

Note: the biserial correlation originated in Karl Pearson, '"On a New Method of Determining Correlation ....", Biometrika, Vol. VII, pp. 96-105, 1909, and the point-biserial correlation originated in Richardson, M.W. & Stalnaker, J.M. (1933). "A note on the use of bi-serial r in test research". Journal of General Psychology, 8, 463-465.

Henrysson, S. (1963). Correction for item-total correlations in item analysis. Psychometrika, 28, 211-218.

Point-biserial fit indices. Stenner AJ. … Rasch Measurement Transactions, 1995, 9:1 p.416

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt91h.htm

Website: www.rasch.org/rmt/contents.htm