Speedy JMLE (UCON) Estimation of Rasch Measures

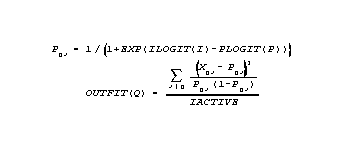
Rasch estimation programs address the incompatible goals of statistical exactness, flexibility, data set capacity and speed. Compromises must be made. Gerhard Fischer's (1974) Rasch computer program features exactness. BIGSTEPS features flexibility and capacity. In real-time instructional use, speed may be the most valuable attribute. Demonstrating Rasch methodology by enabling students to perform many analyses quickly can be more valuable than exactness or flexibility.

I am writing an item analysis program which will go with a French psychometry textbook and probably also an English one. This program implements both classical and Rasch methodology. Flexibility is not important. The data are restricted to dichotomies with no missing responses (a "classical" constraint). Speed is important with capacity the next consideration.

Rasch estimation has the convenient feature that the same raw scores across the same items yield the same measure estimates. When there are L items (with no missing data), there are L+1 possible raw scores: 0,1,..,L. Of these, L-1 measures are estimated directly from the data. The measures for 0 and L can be estimated indirectly by some Bayesian rule, e.g., as the measures for 0.5 and L-0.5. Thus, regardless of how many subjects there are, only L+1 person estimates are required. Similarly, when there are N persons (with no missing data), there are at most N+1 item measures. This leads to computational convenience and the possibility of fast, memory-efficient programs.

PROX (BTD, p. 61-62) is the obvious estimation method, because there is a non-iterative form for complete data. But PROX is based on symmetric, unimodal distributions. My application requires demonstrating the impact of skewed and multi-modal distributions, as well as guessing, copying and other unmodelled activity. So JMLE (UCON) (BTD, p. 63-65) becomes the method of choice. Here is a speedy version of that method, building on the similar approach presented in Wright & Panchapakesan (1969):

Step 1) Cycle through data counting the raw score for every element (person or item). Count up the number of non-extreme items, IACTIVE, and non-extreme persons, PACTIVE. If there are extreme scores for any elements (0 or >=PACTIVE for items, 0 or >=IACTIVE for persons), flag the extreme elements. Cycle through again counting the raw score for every element (person or item) obtained only on non-extreme elements (items or persons). Repeat this until no new extreme elements are identified. Extreme elements will all now have scores of 0 or PACTIVE (for items) and IACTIVE (for persons).

Step 2) Make an entry in table PSCORE for each of the different person raw scores observed on the final set of non-extreme items. In the matching table PFREQ record the number of persons who made each score. These tables have PTABMAX entries with a maximum of IACTIVE+1. Similarly store in table ISCORE each of the observed item raw scores and in matching table IFREQ their frequencies of occurrence. These tables have ITABMAX entries with a maximum of PACTIVE+1.

Step 3) Define tables PEXPECTED, PVAR and PLOGIT to match PSCORE, and tables IEXPECTED, IVAR and ILOGIT to match ISCORE. PEXPECTED and IEXPECTED contain expected score fields. PVAR and IVAR contain variance fields. For each person score, define an initial measure,
PLOGIT(P) = log_e(PSCORE(P) / (IACTIVE - PSCORE(P))).
For each item score, define an initial calibration
ILOGIT(I)=log_e((PACTIVE-ISCORE(I))/ISCORE(I)).
For extreme scores, adjust PSCORE(P) and ISCORE(I) up by 0.5 for scores of 0, and down by 0.5 for perfect scores.

Step 4) Center the non-extreme item calibrations:
ITOTAL=0
FOR I = 1 to ITABMAX
'not extreme score
IF ISCORE(I)>0 and ISCORE(I)<PACTIVE THEN
'sum non-extreme items
ITOTAL = ITOTAL + ILOGIT(I)*IFREQ(I)
ENDIF
NEXT I
'adjustment to center non-extreme items
IMEAN = ITOTAL / IACTIVE
'adjust to new center
FOR I = 1 to ITABMAX: ILOGIT(I) = ILOGIT(I) - IMEAN: NEXT I

Step 5) Initialize the expected score and variance counters:
FOR I = 1 to ITABMAX: IEXPECTED(I) = 0: IVAR(I) = 0: NEXT I
FOR P = 1 to PTABMAX: PEXPECTED(P) = 0: PVAR(P) = 0: NEXT P

Step 6) Compute expected marginal scores and variances corresponding to each raw score:
FOR P = 1 to PTABMAX
FOR I = 1 TO ITABMAX
'expected
PROB = 1 / (1 + EXP(ILOGIT(I) - PLOGIT (P)))
' variance
V = PROB*(1-PROB)
IF PSCORE(P)>0 and PSCORE(P)<IACTIVE THEN
' bypass extremes
IEXPECTED(I)=IEXPECTED(I) + PROB*PFREQ(P)
IVAR(I) = IVAR(I) + V*PFREQ(P)
ENDIF
IF ISCORE(I)>0 and ISCORE(I)<PACTIVE THEN
' bypass extremes
PEXPECTED(P)=PEXPECTED(P) + PROB*IFREQ(I)
PVAR(P) = PVAR(P) + V*IFREQ(I)
ENDIF
NEXT I
NEXT P

Step 7) Compute revised unconditional (joint) maximum-likelihood estimates:
' to save largest change
MAXCHANGE=0
' to save largest raw score residual
MAXRESIDUAL=0
FOR P = 1 TO PTABMAX
' marginal score discrepancy
RESIDUAL = PSCORE(P) - PEXPECTED(P)
IF ABS(RESIDUAL)>MAXRESIDUAL THEN
MAXRESIDUAL = ABS(RESIDUAL)
ENDIF
' Newton-Raphson method
CHANGE = RESIDUAL / PVAR(P)
IF ABS(CHANGE)>MAXCHANGE THEN
MAXCHANGE = ABS(CHANGE)
ENDIF
PLOGIT(P) = PLOGIT(P) + CHANGE
NEXT P
FOR I = 1 TO ITABMAX
RESIDUAL = ISCORE(I) - PEXPECTED(I)
IF ABS(RESIDUAL)>MAXRESIDUAL THEN
MAXRESIDUAL = ABS(RESIDUAL)
ENDIF
CHANGE = RESIDUAL / IVAR(I)
IF ABS(CHANGE)>MAXCHANGE THEN
MAXCHANGE = ABS(CHANGE)
ENDIF
ILOGIT(I) = ILOGIT(I) - CHANGE
NEXT I

Center the ILOGIT(I) item calibrations, as in Step 4 above.

Step 8) Go back and repeat Step 5 onwards until MAXRESIDUAL is less than 0.5 score points, i.e., all residuals are unobservably small, and MAXCHANGE is less than .01 logits, i.e., all changes are unprintably small.

Step 9) The final person measures are PLOGIT(P) with model S.E. of 1/sqrt(PVAR(P), and the final item calibrations are ILOGIT(I) with model S.E. of 1/sqrt(IVAR(I).

Step 10) To compute fit statistics, the original non-extreme response strings must be accessed. For an OUTFIT mean-square, consider non-extreme person Q, with observed score recorded at PSCORE(P). This person has measure PLOGIT(P). Q's response to non-extreme item J is XQJ. Item J has observed score ISCORE(I) and calibration ILOGIT(I). Q's expected response to item J is PQJ. Then,

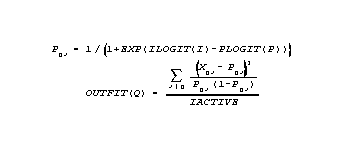
Programmers will discover ways to optimize this code for particular languages and applications. Comparing this speed- oriented approach with the flexible approach used by BIGSTEPS (no slouch itself) reduced the time required for an analysis of 30 items and 400 persons from 19.2 seconds to 1.0 seconds on my target hardware.

BTD: Wright BD & Stone MH (1979) Best Test Design. Chicago: MESA Press.

Fischer G (1974) Introduction to Mental Test Theory. Bern: Huber.

Wright, B. D., and Panchapakesan, N. A. 1969. A procedure for sample-free item analysis. Educational and Psychological Measurement 29: 23-48

Speedy UCON estimation of Rasch measures. Peladeau N. … Rasch Measurement Transactions, 1995, 9:1 p.418

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt91k.htm

Website: www.rasch.org/rmt/contents.htm