Teams, Packs and Chains

In the 1920's Physicist Norman Campbell considered linear measurement of a social science variable to be impossible because he thought people could not be concatenated in any way similar to placing sticks end-to-end to measure length. More recently we have come to realize that people are always being "concatenated", i.e., accumulated to increase quantity according to specific rules. Teams, Packs and Chains are three methods of social concatenation.

Teams:
Teams work as unions of perfect agreements. When Team members are given a task to perform, they must all agree on what to do (right or wrong). For a two-member team, helpful agreement (11) wins, but unhelpful agreement (00) loses. Disagreements (10) and (01) are absent because they are eliminated by the rules that define Team behavior. Let Team concatenation be indicated by x.

If Pni is the probability of success of person n on item i, and Pmi is the probability of success of person m on item i, then their Team odds of success, under Rasch model conditions, is:

(Pnxm/(1-Pnxm)) = Pni*Pmi / (1-Pni)*(1-Pmi)

= exp (Bn+Bm -(Di+Di))

Take logs and generalize to N Team members. Define N-member Team strength as BT. Then

BT - Di = sum (Bn - Di)

The strengths of individual Team members relative to task difficulty (Bn - Di) add up to Team strength relative to task difficulty, (BT - Di). Teams are concatenations of relative strengths, accumulated in linear form. Adding a member more able than the task increases Team strength. Adding a member less able than the task decreases Team strength and weakens the Team. More is often not better, as has been frequently observed about committees.

Packs:
Packs work as collections of helpful disagreements. When Pack members are given a task to perform, the first success wins for the Pack. If no member is successful, the Pack loses. Search- parties work this way. For a two-member Pack, helpful disagreements (10) and (01) win. Unhelpful agreement (00) loses. Helpful agreement (11) is absent because it is eliminated by the rules that define Pack behavior. Let Pack concatenation be indicated by +.

If Pni is the probability of success of person n on item i, and Pmi is the probability of success of person m on item i, then their Pack odds of success, under Rasch model conditions, is:

Pn+m/(1-Pn+m) = ( Pni(1-Pmi) + (1-Pni)Pmi ) / (1-Pni)(1-Pmi) exp(Bn+m) = exp(Bn) + exp(Bm)

a concatenation of absolute strengths accumulated in exponential form, which does not depend on Di.

When Bn and Bm are similar, this is approximated by:

exp(Bn+m) = 2 exp ((Bn + Bm)/2)

Take logs and extend to N similarly able Pack members. Define N- member Pack strength as BP. Then

BP = sum (Bn/N) + log_e(N)

Pack composition is a collection because the helpful disagreements of Pack members collect to benefit the Pack. As N rises so must BP. The more the better. Unlike Teams, the strength of a Pack is independent of task difficulty.

Chains:
Chain composition is a connection of commitments against harmful disagreement. Member actions are linked by mutual reliance on not disagreeing. An ability to maintain complete agreement is Chain strength. The harm that can result from a single disagreement is Chain weakness.

When the Chain members are given a task to perform, the first failure loses for the Chain. If there is no failing member, the Chain wins. For a two-member Chain, helpful agreement (11) wins. Lack of agreement (10) and (01) loses. Unhelpful agreement (00) is absent because it is eliminated by the rules that define Chain behavior. Let Chain concatenation be indicated by *.

If Pni is the probability of success of person n on item i, and Pmi is the probability of success of person m, then their Chain odds of success, under Rasch model conditions, is:

Pn*m/(1-Pn*m) = Pni*Pmi /( Pni(1-Pmi) + (1-Pni)Pmi )

exp(-Bn*m) = exp(-Bn) + exp (-Bm)

a concatenation of weaknesses accumulated in exponential form, which does not depend on Di.

When Bn and Bm are similar this is approximated by:

exp(Bn*m) = 0.5 * exp((Bn+Bm)/2)

Take logs and extend to N similarly able Chain members. Define N-member Chain strength as BC. Then

BC = sum (Bn/N) - log_e(N)

Adding another member or link to a Chain always decreases Chain strength.

Comparison:
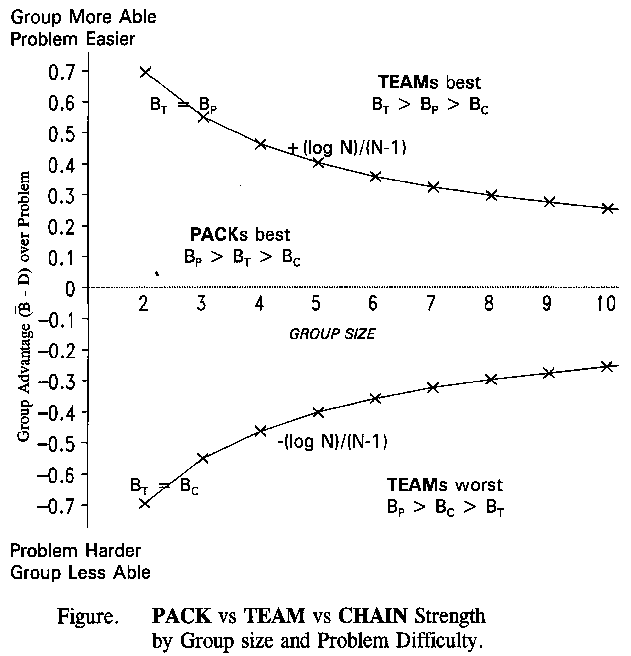
The Figure depicts the effectiveness of the three types of concatenation as group size (of equally able members) increases for a range of problem difficulties.

Example: Imagine there are 10 people, all of ability -1 logit relative to the task to be performed:
Team ability = B_T = 10 * -1 = -10 logits
Pack ability = B_P = 10 * (-1 / 10) + log_e(10) = 1.3 logits
Chain ability = B_C = 10 * (-1 / 10) - log_e(10) = -3.3 logits
so that: B_P > B_C > B_T

Teams are most effective when a problem is very easy (at the top), otherwise Packs are most effective. Chains are least effective, except when a problem is very hard (at the bottom). Then Teams are least effective. A mob is a Team that chooses the wrong solution to a difficult social problem.

On a practical note, productive Japanese-style consensus- building, i.e., Team-work, requires that each difficult task be divided into several easy tasks, so that there is a high probability that each group member, acting alone, would have made the consensus-decision.

Teams, packs and chains. Wright BD. … Rasch Measurement Transactions, 1995, 9:2 p.432

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt92j.htm

Website: www.rasch.org/rmt/contents.htm