Cronbach Alpha, KR-20, True-Score Reliability or Rasch Reliability?

Rasch Person Separation Reliability (RR) is sometimes noticeably lower than the True-Score (KR-20, Cronbach Alpha) Reliability (RT). Why?

RR and RT estimate the same coefficient:

Reliability = Trait Variance / Observed Variance

where Trait Variance refers to the unobservable, hence fictional, "true" variance of the persons on the underlying trait. Observed Variance compounds trait variance, measurement error, data misfit and other anomalies. Reliability indicates the stability of person measures or scores under hypothetical replications of equivalent tests.

Zero and Perfect Extreme Scores
In classical True-Score test theory (CTT), perfect and zero scores are modelled to be exact. They have no error variance. Consequently including extreme scores lowers the average score error and inflates RT. In Rasch theory, an extreme score is recognized as containing little information about that person's location on the infinite latent trait. Any arbitrary "measure" set to correspond to such a score has an infinitely large standard error. Thus, including persons with extreme scores increases the average measurement error and lowers RR.

Statistical Validity
Statistical "validity" is the correlation between the person measures or scores on a test and those persons' unobservable, and hence fictional, exact trait measures. Clearly, if we are interested in estimating a person's math ability, we are more concerned about locating that person on the trait (statistical validity) than in having that person obtain a stable measure or raw score (reliability).

At first glance, better reliability must lead to better validity. In fact, one might predict that
Reliability coefficient = (Validity coefficient)^2
But this is true only up to a point. When better reliability means worse validity, we have the famous "Attenuation Paradox" (RMT 6:4, p. 257).

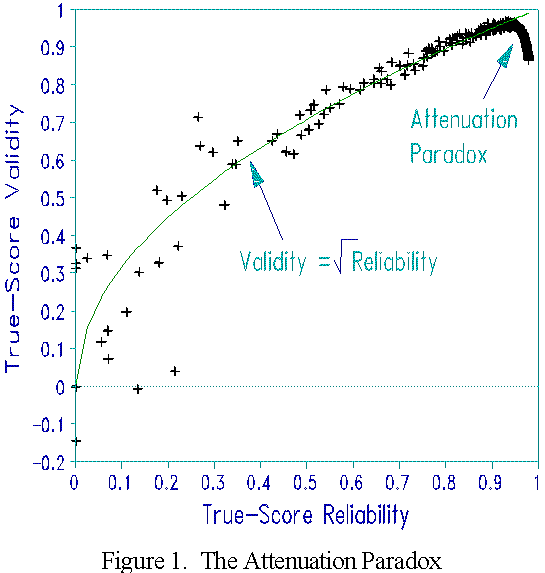
Figure 1 depicts the attenuation paradox. In a simulation study, a test was constructed containing 40 dichotomous items uniformly distributed across a two logit range. This was administered to 1000 normally distributed, on-target samples of 114 persons with trait S.D.'s uniformly distributed from 0 to 9.99 logits under Rasch model conditions. True-Score reliability and validity coefficients were calculated for each sample and plotted. In this case, validity is the correlation between the simulated person scores and their generating logit ability values. In Figure 1, validity and reliability follow their predicted relationship over most of their range. For high reliability values, however, validity drops! (For the same result using a normal ogive model, see Sitgreaves, 1961).

Rasch reliability and validity coefficients were also computed. For zero and perfect scores, Rasch measures corresponding to 0.5 score-points from the extreme were estimated. The Rasch validity coefficient for each sample is the correlation between generating and estimated persons measures. The reported Rasch reliability coefficient is the misfit-attenuated "real" version.

Figure 2 shows the trend lines. Corresponding Rasch and True-Score coefficients are almost identical for samples up to 1 logit S.D. This is to be expected, because, when all scores are central, the ogival relationship between scores and measures is close to linear. Beyond this point, however, results differ markedly.

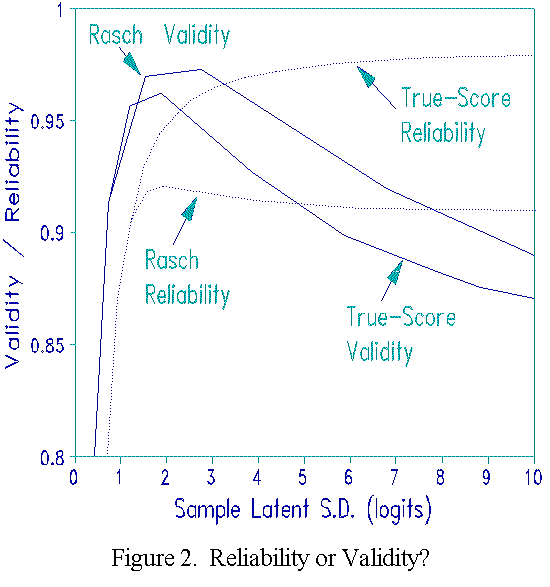
True-Score validity levels off and then starts dropping after 2.0 logits S.D. As the ability range becomes wider, the non-linear compression of the widening range of abilities into a narrow range of scores lowers the correlation between scores and trait location, and so lowers the True-Score validity. Rasch validity continues to increase until the sample S.D. is 3.0 logits. Beyond this, the test becomes too easy or too hard. It cannot locate many persons on the trait, so validity drops. Since Rasch validity is generally higher than True-Score validity, Rasch is more effective than raw scores at locating persons on the underlying trait.

The Attenuation Paradox
Rasch person separation reliability also increases up to 2.0 logits S.D., then drops off slowly. The person ability range is now very wide, so that persons at the ends of the range are measured very imprecisely by the test. The increase in the underlying ability range is counteracted by the increasing imprecision in the outlying measures so that Rasch reliability decreases slowly.

True-Score reliability, however, increases monotonically with person trait variance. This indicates that as sample dispersion becomes greater, individual raw scores become more stable (i.e., the data become more Guttman-like). But the decrease in True- Score validity means that these scores are less useful for locating persons on the latent trait. We know more and more about less and less. Perfect True-Score reliability is obtained when all items are perfectly correlated, i.e., acting like one item. Such a test has the statistical validity of a one item test, i.e., almost none.

"For the ordinal data, when the sample sizes increases, on average the estimated alpha [true-score reliability] overestimates the true value of alpha." (Tsagiris et al., 2013)

True-Score Reliability or Rasch Reliability?
Contrary to popular belief, the conventional True-Score reliability coefficient does not always summarize the measurement effectiveness of a test. Regardless of the relative sizes of the reliability coefficients, Rasch measures are more useful than raw scores for locating persons on an underlying trait.

Sitgreaves R (1961) A statistical formulation of the attenuation paradox. In Solomon H. (Ed.) Studies in Item Analysis and Prediction. Stanford, CA: Stanford University Press.

Tsagris,M., Frangos,Con. C. and Frangos, C.C. (2013). Confidence intervals for Cronbach's reliability alpha coefficient. Proceedings of the Third International Conference on Quantitative and Qualitative Methodologies in the Admin. and Econ. Science. Athens, 24-25 May, 2013.

Cronbach Alpha, KR-20, True-Score Reliability or Rasch Reliability? Linacre JM. … Rasch Measurement Transactions, 1996, 9:4 p.455

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt94a.htm

Website: www.rasch.org/rmt/contents.htm