Choosing Sample Distributions

Sample distributions bear a paradoxical relationship to measurement. On the one hand, they often simplify estimation or may even be required to make estimation possible. On the other hand, surely my measure should not depend on the distribution of the sample I happen to be measured with! It is clearly preferable,whenever possible, to use estimation methods that do not require person or item distributions to be specified.

The simplest sample distribution is the point distribution, hypothesizing a fixed effect. Everyone is thought to have the same amount of the attribute - but how much? Many attitude surveys are conceptualized this way. See RMT 5:4 p. 188 for an example using log-linear and one-facet logit-linear Rasch models.

When a population is thought to be represented by a central value, but individuals differ from that value in innumerable ways, each constituting a small amount, then the normal distribution is often chosen. ANOVA techniques use the normal distribution implicitly, usually without any type of fit test. The degree to which the normal distribution can simplify estimation is seen in Cohen's PROX algorithm which obtains a direct analytical solution in a situation that usually requires a non-linear, iterative approach (RMT 8:3 p. 378). Marginal maximum likelihood (MMLE) methods employ the normal distribution, sometimes to simplify estimation, sometimes to make it possible. Thus, for the 2- and 3-parameter IRT methods, a normal (or other) distribution must always be specified.

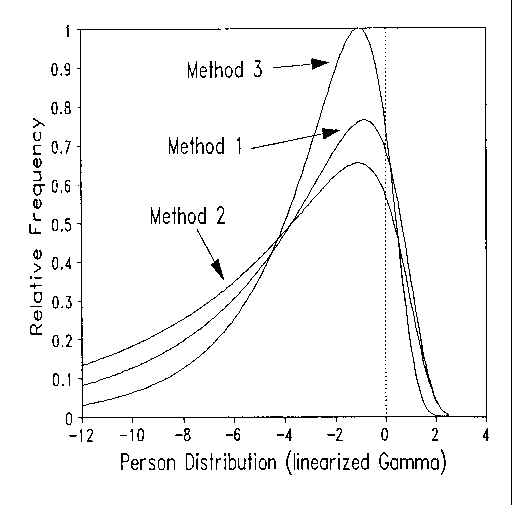
Some sample distributions are chosen strictly on their mathematical properties regardless of the empirical sample distribution. If a global test yields some degree of model-to-data fit, then the chosen distribution is accepted as representing that sample distribution. Thus, van Duijn and Jansen (1995) choose a gamma distribution for their subjects and a Dirichlet distribution for their items, becausethese produce a tractable marginal maximum likelihood estimation function for theirPoisson count data. The Figure depicts the modeled ability distributions of the pupils in their three reading-method groups.

Actual distributions can be skewed, squashed, lumpy,... Before investing effort in the analysis or estimation of a particular mathematical distribution function, it is wise to rough out histograms of the person and item score distributions (on semi-log_e paper if the data are Poisson counts). Then make an informed choice of distribution. For instance, if the data are seen to be multimodal, then a uniform distribution is probably a better choice than a normal distribution (see Wright & Stone's Best Test Design p. 145 ff. for computer-free use of the uniform distribution). Once the computer has printed estimates based on your selected distribution, it is hard to admit to oneself that one has made a poor, or even misleading, choice of distribution(See RMT 5:3 p.172 for an example of how easy it is to convince oneself that a particular distribution's shape is "correct").

John M. Linacre

Van Duijn M.A.J., Jansen M.G.H. (1995) Modeling repeated count data: some extensions of the Rasch Poisson Counts model. Journal of Educational and Behavioral Statistics 20:3, 241-258.

Linacre J.M. (1996) Choosing sample distributions. Rasch Measurement Transactions 10:2 p. 503

Choosing sample distributions. Linacre J.M. … Rasch Measurement Transactions, 1996, 10:2 p. 503

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt102f.htm

Website: www.rasch.org/rmt/contents.htm