KR-20 / Cronbach Alpha or Rasch Person Reliability: Which Tells the "Truth"?

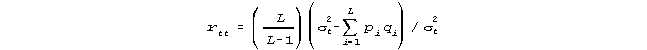
"The reliability of any set of measurements is logically defined as the proportion of their variance that is true variance... We think of the total variance of a set of measures as being made up of two kinds of variance: true variance and error variance... The true measure is assumed to be the genuine value of whatever is being measured." (Guilford, 1965, p. 488). So,

and, when measures and errors are uncorrelated,

Thus "reliability" is not an index of quality ("Is this a good measure of ...?"), but of relative reproducibility ("How repeatable is this measure?"). The most popular estimator of raw-score reliability is the Kuder-Richardson 20, a special case of Cronbach's Alpha:

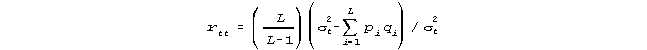
where L is the length of the test, ²_t is the variance of test raw scores across subjects, p_i is the number of subjects who succeeded on item i, and q_i is the number of subjects who failed. σ²_t is the observed variance. pq estimates a binomial error variance. KR-20 is an index of the repeatability of raw scores, misinterpreted as linear measures.

The focal question is "Does this test produce repeatable measures for this sample?" The observed variance is of the Rasch measures. Each observation is modeled to include error:

X_ni=0,1 is the response by subject n to item i. P_ni is the probability that subject n would succeed on item i. P_ni(1-P_ni) is the binomial variance of an observation like X_ni. The error variance of Rasch measures is estimated from the sum of the modeled variance of observations. This "model" error variance requires the data to conform stochastically to the Rasch model. Since there is always additional noise in the data, a more "real" error variance is:

"Real" error variance = model variance * MAX(1.0, INFIT mean-square)

Rasch reliability = (observed measure variance - "real" error variance) / observed measure variance

How does test targeting affect reliability? A test of 50 dichotomous items, uniformly distributed from -2 to +2 logits, was simulated on hypothetical samples of 1,000 subjects with abilities distributed, N(0,1). The sample was initially targeted on the test, then mistargeted one-half logit away from the test in five successive steps. This was repeated three times and their means reported.

For each targeting, KR-20 and "true" raw score S.D. were computed.

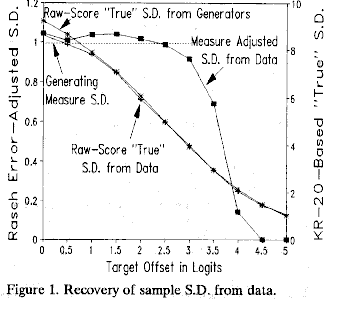
In Figure 1, the raw score S.D.s (using the right-hand Y-axis) are highly offset-dependent, but approximate the values predicted from the generating measures over the entire range.

For Rasch reliabilities, Adj. S.D. estimates the generator, "true", S.D.: Adj. S.D. = observed measure S.D. * (reliability). Zero and perfect scores were replaced by scores 0.5 score points more central, and the corresponding measures and standard errors imputed. In Figure 1, the success of the recovery of the generating measures from the simulated data is shown by the Adjusted S.D. curve. The recover is reasonably accurate with offsets in the range 0 to 3 logits.

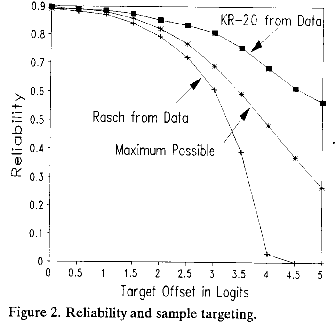Rasch reliabilities can also be computed directly from the generating measures and item difficulties without data. These generator-based reliabilities are the maximum possible. Figure 2 plots all three reliability coefficients against the target offsets. As offset increases, the proportion of extreme scores increases and all reliabilities decrease. Rasch data-based reliabilities are less than the generator-based reliabilities because (i) measures are estimated from discrete (not continuous) raw scores; (ii) measures for extreme scores are biased towards the test center as targeting becomes more offset; (iii) Rasch S.E.s are INFIT-inflated, (but this is a minor effect). Thus Rasch data-based reliability understates measure reliability, providing assurance that a test has performed at least as well as Rasch "real" reliability.

KR-20 (Cronbach Alpha) always exceeds the maximum reliability possible for the measures underlying these simulated data. This misleads the test-user into believing a test has better measurement characteristics than it actually has. Yet KR-20 has met its design criteria, because estimated raw-score "true" S.D.s in Figure 1 match their predicted values. It reports the reliability of raw scores accurately, but these are local, test-dependent rankings. KR-20 overstates the reliability of the test-independent, generalizable measures the test is intended to imply. For inference beyond the test, Rasch reliability is more conservative and less misleading.

There is much more at RMT 13:2 Relating Cronbach and Rasch Reliabilities

John M. Linacre

Guilford J.P. (1965) Fundamental Statistics in Psychology and Education. New York: McGraw-Hill.

KR-20 / Cronbach Alpha or Rasch Person Reliability: Which Tells the "Truth"? Linacre J.M. … Rasch Measurement Transactions, 1997, 11:3 p. 580-1

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt113l.htm

Website: www.rasch.org/rmt/contents.htm