Relating Cronbach and Rasch Reliabilities

"My question has to do with the Rasch person separation reliability.

(1) Can you tell me how it is calculated?

I've noticed that sometimes the Rasch-based reliability is essentially identical to Cronbach's alpha and sometimes it isn't.

(2) Are there limitations on how Rasch separation reliability is to be interpreted?

This arises because with alpha it is necessary that the measures be independent. For example, if two raters rate a group of examinees on five tasks (so that I have ten data points for each examinee, two per task), I will need to sum or average the ratings within task. If I use all ten data points to calculate alpha, it is likely to be substantially inflated."

Brian Clauser

Cronbach's alpha, KR-20, and the separation reliability coefficients reported in a Rasch context are all estimates of the ratio of "true measure variance" to "observed measure variance".

For all these methods, the basic underlying relationship is specified to be:

For Cronbach's alpha, computed from non-linear raw scores, an estimating equation is:

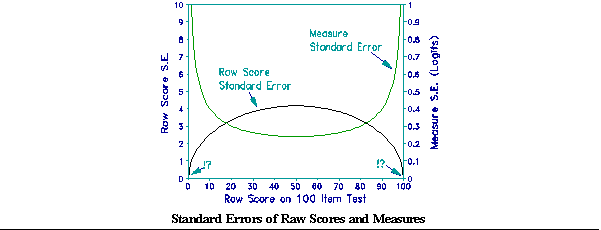
where k is the number of observations per examinee, σ² is the raw score variance across examinees, and σ_i² is the raw score variance for observation i across examinees. Generalizability Theory addresses the situation in which every rater does not rate every examinee on every item and task. Extreme scores are usually included. Since extreme scores have no score error variance, their effect is to increase the reported reliability.

For Rasch separation reliability, computed from linear measures, an estimating equation for N examinees is

Extreme scores are usually excluded, because their measure standard errors are infinite.

There is much more at RMT 11:3 KR-20 / Cronbach Alpha or Rasch Reliability: Which Tells the "Truth"?

Both of these estimation methods disregard covariance between raters, items, tasks, etc. But some covariance always exists. Usually not enough to merit special attention. Suppose, however, that your raters are not acting as independent experts, but rather as "rating machines". Then using two or three raters would be the same as running an MCQ form through two or three optical scanners. There would be near-perfect covariance between the raters. Under these conditions, more raters, just like more optical scanners, would not increase test reliability.

If you suspect rater covariance, you could obtain a lower bound for the separation reliability by estimating the reliability as if there were only one rater per subject:

where R is the reported reliability and N is the number of raters rating each examinee.

For instance, if the reported separation reliability with 5 raters is 0.83, and you suspect that raters are being forced into agreement, then a more reasonable separation reliability is that with one rater:

Relating Cronbach and Rasch Reliabilities Clauser B., Linacre J.M. … Rasch Measurement Transactions, 1999, 13:2 p. 696

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt132i.htm

Website: www.rasch.org/rmt/contents.htm