Notes and Quotes: RMT21:4

Rasch as a World-View

Rasch measurement is really about a more powerful way of thinking about the world around us. Rasch models imagine the world to be composed of perfect equal-interval latent variables. These express the meaning in everything that is around us. We can reconstruct the perfect variables from imperfect data. The perfect variables give us great insights into why things are the way they are. Their use gives us the security that comes from knowing what will probably happen. They even gives us power to change the future. All this sounds impossible, far out of the reach of mere humans. But "You have to believe the impossible" (Howard Head, inventor of Head skis and Prince tennis rackets). Rasch measurement is about the impossible.

John Michael Linacre

Journal of Applied Measurement

Volume 9, Number 2. Summer 2008

Effects of Varying Magnitude and Patterns of Response Dependence in the Unidimensional Rasch Model. Ida Marais and David Andrich

Fisher's Information Function and Rasch Measurement. Mark H. Stone

A Rasch Analysis for Classification of Systemic Lupus Erythematosus and Mixed Connective Tissue Disease. Kyle Perkins, Robert W. Hoffman, and Nikolaus Bezruczko

Magnitude Estimation and Categorical Rating Scaling in Social Sciences: A Theoretical and Psychometric Controversy. Svetlana Beltyukova, Gregory E. Stone, and Christine M. Fox

Impact of Altering Randomization Intervals on Precision of Measurement and Item Exposure. Timothy Muckle, Betty Bergstrom, Kirk Becker, and John Stahl

Rasch Measurement in Developing Faculty Ratings of Student s Applying to Graduate School. Sooyeon Kim and Patrick C. Kyllonen

Understanding Rasch Measurement: Using Rasch-Scaled Stage Scores to Validate Orders of Hierarchical Complexity of Balance Beam Task Sequences. Michael Lamport Commons, Eric Andrew Goodheart, Alexander Pekker, Theo Linda Dawson, Karen Draney, and Kathryn Marie Adams

Richard M. Smith, Editor

JAM web site: www.jampress.org
JAM library recommendation form

IRT and The Rasch Model in Disguise

"The three-parameter logistic (3PL) model (...) was used to analyze item responses on the multiple choice items. For analysis of the constructed response items, the two-parameter partial credit model (2PPC) (...) was used." (pp. 8-9)

"In IRT, all the item characteristic curves for the items on a test can be added together to yield a function - the test characteristic curve (TCC) - that shows the expected raw score for each given scale score. By inverting the TCC, an expected scale score can be computed for each raw score. This new function - the inverse of the TCC - can be summarized in an RS-SS table. An advantage of RS-SS tables is that they make scoring relatively straightforward: With number-correct scoring, it is sufficient to know how many raw score points a student obtained on the test to determine a student's scale score." (p. 19)

New York State Testing Program. Mathematics Grade 8. Technical Report 2003.

Comment: "sufficient to know how many raw score points" is a criterion for the Rasch model: RMT 3:2 p. 62.

https://www.rasch.org/rmt/rmt32e.htm

By setting up a one-to-one correspondence between raw scores and scale scores, New York State approximated the Rasch model and, as they say, this is "an advantage"!

The Truth about IRT Scaling

"The [2-PL, 3-PL] theta-scale, or any linear transformation of it, however, does not possess the properties of a ratio or interval scale, although it is popular and reasonable to assume that the theta-scale has equal-interval properties"

Hambleton, Swaminathan and Rogers, "Fundamentals of Item Response Theory", 1991, p.87.

"Liking for Science" - the inside scoop!

The book "Rating Scale Analysis" (Wright & Masters, 1982) features a data set in which 75 children give their reaction to 25 items relating to science activities. Julian Mingus (Ph.D., U. Toledo, 1975) was in the Dept. of Education at Cleveland State University, Cleveland, Ohio, when he conducted the data collection. He remembers that both boys and girls were in the study at the Cleveland Museum of Natural History. They had mixed ethnicity. Their families were of lower to middle socio-econimic status and their grade levels were probably 1st to 6th (6 yrs - 11 yrs) .

Mingus co-authored "Comparative perceptions of Elementary, Junior High, and Senior High school principals on selected work related variables." Brent Poppenhagen, Julian Mingus, Joseph Rogus. Journal Of Educational Administration, 1980, 18, 1, 69 - 87

One of his interests in photography:

www.jmingus.com/

Courtesy of Christine Fox, U. Toledo

Rasch Measurement SIG, AERA

Annual Report 2007-2008

At the Rasch Measurement SIG Business Meeting at the AERA Annual Meeting, New York, 2008, Secretary/Treasurer Ed Wolfe summarized the current status of the SIG.

Membership: There are currently 197 members, an increase of 59 in the last year with 87 lapsed memberships.

Finances: The January 2008 balance of the SIG account is $8,649.10, an increase of $2,281.95 since January of 2007.

Officers: Ed Wolfe was nominated (unopposed) and appointed to the office of Chair of the SIG, and Timothy Muckle was nominated (unopposed) and appointed to the office of Secretary/Treasurer. Dimiter Dimitrov and Diana Bernbaum were appointed as the SIG's 2009 Program Co-Chairs. John Michael Linacre will continue as the Editor of Rasch Measurement Transactions. William Fisher was appointed to an ad hoc committee to explore the development of SIG-sponsored awards.

Invitation: William Fisher introduced the idea of developing SIG-sponsored awards. Anyone interested in being a member of this ad hoc committee should contact Ed Wolfe (edwolfe ~at ~ vt.edu).

ConstructMap

formerly GradeMap

ConstructMap is a graphical, menu-driven software package that combines a multidimensional IRT and Rasch engine for estimating item and person parameters with tools for managing cross-sectional and longitudinal student response data and interpreting findings from such data. Graphical maps and reports are designed for use in settings in which progress on multiple measures can be examined and analyzed. Users can select expected-a-posteriori (EAP), maximum likelihood, or plausible value estimates of multivariate proficiency estimates. ConstructMap accepts dichotomous, rating scale, or partial credit items with between-item (each response is an indicator of a single dimension) or within-item (a response may be an indicator of multiple dimensions) multidimensional models.

http://bearcenter.berkeley.edu/GradeMap

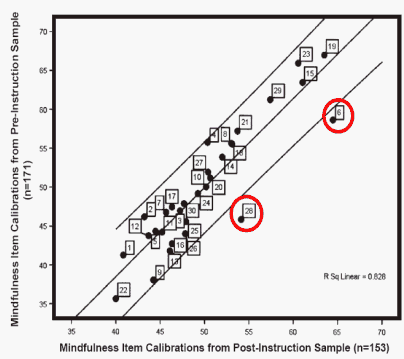
"Omitting the items [6, 28] from the scale makes virtually no difference in the resulting measures, suggesting that there is no substantive significance to the items' statistically significant changes in position."

Solloway, S.G., & Fisher, W.P. (2007) Mindfulness in Measurement. International Journal of Transpersonal Studies, 26, 58-81

Case-Control Studies

"Statistically, the Rasch model we outline is equivalent to the 'conditional logit model' or the 'conditional logistic regression for matched case-control groups model', as it is referred to by statisticians and epidemiologists. It can be estimated using a conditional maximum likelihood method."
Gautschi, T. (2001, March). Trust over time: The effects of dyadic social capital., Department of Sociology, Utrecht University, The Netherlands.

"This article presents new results on the standard techniques used in analysis of data from Rasch models, and the special case of Rasch models typically used with data from matched case-control studies."
Rice, K. M. (2004). Equivalence between conditional and mixture approaches to the Rasch model and matched case-control studies, with applications. Journal of the American Statistical Association, 99(466), 510-22.

Courtesy of William P. Fisher, Jr

Misfitting Observations

"When you have something simple that agrees with all the rest of physics [i.e., all the rest of the latent trait] and really seems to explain what is going on, a few experimental data against it are no objection whatsoever."

Nobel Laureate Murray Gell-Mann (1969, Physics) quoted in "The Evidential Power of Beauty: Science and Theology" (Thomas Dubay), p. 115.

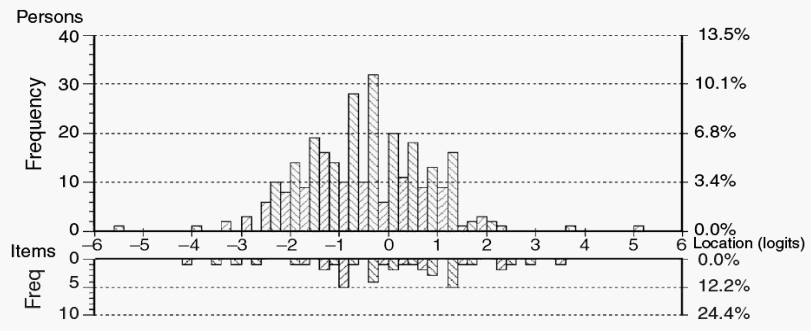
Person and item distribution graph for Total HADS Psychological Distress Scale.

Pallant F. & Tennant A. (2007) an introduction to the Rasch measurement model: An example using the Hospital Anxiety and Depression Scale (HADS). British Journal of Clinical Psychology, 46, 1-8.

Notes and Quotes: RMT21:4 … Rasch Measurement Transactions, 2008, 21:4

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt214c.htm

Website: www.rasch.org/rmt/contents.htm