Dichotomous Rasch Model derived from Counting Right Answers:
Raw Scores as Sufficient Statistics

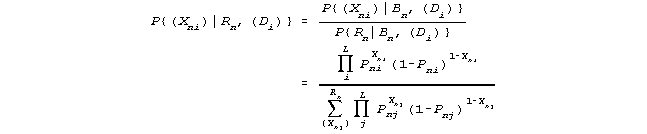
In statistical terminology, "sufficient" means "all the information that this dataset has about ...". So, from a Rasch perspective, the "raw score" has all the information there is in the dataset about the "ability" of the respondent. This is also the Classical Test Theory perspective. But this is not the 2-PL or 3-PL perspective. They say that the "pattern of responses" has all the information there is in the dataset about the "ability" of the respondent.

1. Person n of ability B_n responds to test items (i) with difficulties (D_i) with scored (0,1) responses (X_ni). For the raw score R_n = ΣX_ni to be sufficient for estimating ability, indeed, for counting right answers to be useful at all, R_n must extract ability B_n out of (X_ni).

2. Bayes says that the probability of person n's response vector, given person ability B_n and items of difficulty (D_i), is the probability of the response vector given the raw score R_n multiplied by the probability of the raw score given the ability:

P{(X_ni)|B_n,(D_i)} = P{(X_ni)|R_n,(D_i)} * P{R_n|B_n,(D_i)}

3. If P_ni = f(n,i) is the probability that n succeeds on i, then we can obtain the probability of person n's method of obtaining a score of R_n, and also all other methods of obtaining the same score.

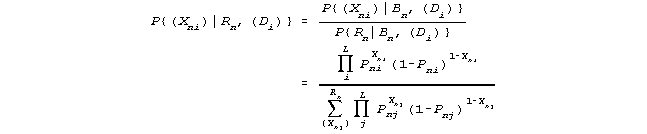
4. R_n points unequivocally to ability B_n only if P{(X_ni)|R_n, (D_i)}, the probability of the particular responses given the raw score, is entirely free from variation due to B_n. Thus the remainder must be locally independent of B_n so that it does not matter which particular (X_ni) are 1's and which are 0's provided that ΣX_ni = R_n. Thus the effect of B_n on the (X_ni) can be factored out of (3) and cancelled.

[This is saying that the set of response vectors are locally independent given the person abilities and the item difficulties. Georg Rasch called this property "specific objectivity".]

5. A sufficient factoring is obtained by asserting that

C_ni = B_n + D_i,

P_ni = B_n / C_ni, and 1- P_ni = D_i / C_ni, then

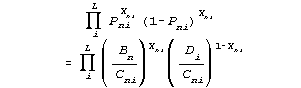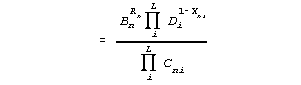so that

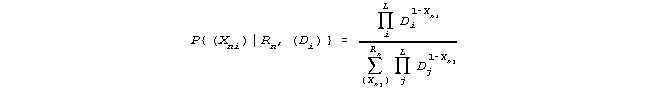
is seen to be free of B_n.

6. Thus a sufficient parameterization is

Reparameterizing,

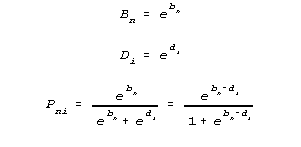
produces the Rasch model, showing that this form of f(n,i) supports the use of R_n for estimating the ability of person n.

7. The necessity of this formulation can be demonstrated by dividing the numerator into the denominator in (3) to produce the following term in the denominator, which must not vary with Bn:

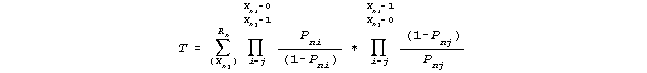
8. In T there are the same number of P_ni and P_nj terms in each product, because the raw score is invariant across the summation. The general condition for T not to vary with Bn, (apart from irrelevant specifics, such as when P_ni and P_nj are constants), is that

which takes us to step (2) of Model Necessary for a Thurstone Scale, RMT 2:1 p. 9-10, and thence to the Rasch model as the necessary f(n,i).

Benjamin D. Wright

Note: Since most of Classical Test Theory (CTT) regards the raw scores as sufficient for decision-making, CTT implicitly assumes that the Rasch model holds for their data.

Dichotomous Rasch Model derived from Counting Right Answers: Raw Scores as Sufficient Statistics. Wright BD. … Rasch Measurement Transactions, 1989, 3:2 p.62

1. The Rasch Model derived from E. L. Thorndike's 1904 Criteria, Thorndike, E.L.; Linacre, J.M. … 2000, 14:3 p.763
2. Rasch model derived from consistent stochastic Guttman ordering, Roskam EE, Jansen PGW. … 6:3 p.232
3. Rasch model derived from Counts of Right and Wrong Answers, Wright BD. … 6:2 p.219
4. Rasch model derived from counting right answers: raw Scores as sufficient statistics, Wright BD. … 1989, 3:2 p.62
5. Rasch model derived from Thurstone's scaling requirements, Wright B.D. … 1988, 2:1 p. 13-4.
6. Rasch model derived from Campbell concatenation: additivity, interval scaling, Wright B.D. … 1988, 2:1 p. 16.
7. Dichotomous Rasch model derived from specific objectivity, Wright BD, Linacre JM. … 1987, 1:1 p.5-6

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt32e.htm

Website: www.rasch.org/rmt/contents.htm