Rasch Model derived from Campbell Concatenation: additivity, interval scaling

Can mental testing meet physicist Norman Campbell's "concatenate heads" requirement for fundamental measurement, namely that the combination of X and Y be more than X or Y, and that X and Y concatenate to produce an X+Y result, interpretable as a physical addition operation? Campbell's concatenation follows strict rules. When a rod of length X is "added" (in a specific way denoted by Ð ) to a rod of length Y, then their combined length is X+Y, i.e.,

In psychological measurement, what happens to the probability of a right answer when two persons, m and n of abilities B_n and B_m, join forces to agree on an answer to item i of difficulty D_i?

Let P_ni be the probability that person n succeeds on item i. Then

also

Are two heads better than one when both are smarter than the item, i.e., both X and Y are positive, so that P_ni>0.5 and P_mi>0.5? Yes, because, since they agree on the answer, the probability space is limited to both succeeding or both failing:

This consensus, "team-work", approach to problem solving is often used by committees. It succeeds admirably provided that each individual committee member has a better than 50% chance of coming to a correct decision.

Can person abilities be concatenated? Yes, because the probability that persons n and m succeed or fail on item i when combined as a team produces:

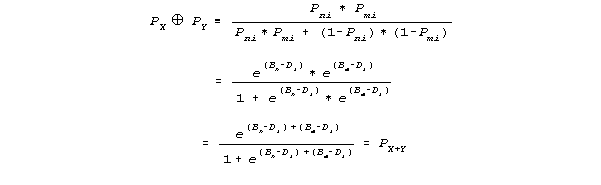
Thus the Rasch probability of a right answer when two persons work together depends on the concatenations of the difficulty of item D_i with the abilities of the two persons, B_n and B_m. The relation

is a concatenation of abilities on the interval scale defined by

What happens when one person is faced with two items, i and j, combined in such a way that the person either succeeds on both or fails on both? Is the combination of two hard items harder than one? Yes, because P_ni<0.5 and P_nj<0.5, so that:

Can item difficulties be concatenated? Yes, in the same way as person abilities. The Rasch probability of getting two items correct depends on the concatenations of the ability of the person, B_n, with the difficulties of the two items, D_i and D_j, producing

Can item difficulties be added to equate person abilities? Yes, because, when P_ni follows the Rasch model, the addition necessary to make the performance of person n on item i appear stochastically equivalent to the performance of person m on the same item i is:

1) pair up another item j with each item i for person n.

2) choose item j such that its difficulty is

3) consider for person n only those cases in which person n succeeds or fails on both i and j, the probability of success (or failure) of person n on items i and j combined becomes

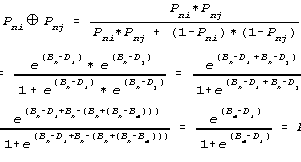
i.e., equivalent to person m on item i.

Benjamin D. Wright

Rasch model derived from Campbell concatenation: additivity, interval scaling. Wright B.D. … Rasch Measurement Transactions, 1988, 2:1 p. 16.

1. The Rasch Model derived from E. L. Thorndike's 1904 Criteria, Thorndike, E.L.; Linacre, J.M. … 2000, 14:3 p.763
2. Rasch model derived from consistent stochastic Guttman ordering, Roskam EE, Jansen PGW. … 6:3 p.232
3. Rasch model derived from Counts of Right and Wrong Answers, Wright BD. … 6:2 p.219
4. Rasch model derived from counting right answers: raw Scores as sufficient statistics, Wright BD. … 1989, 3:2 p.62
5. Rasch model derived from Thurstone's scaling requirements, Wright B.D. … 1988, 2:1 p. 13-4.
6. Rasch model derived from Campbell concatenation: additivity, interval scaling, Wright B.D. … 1988, 2:1 p. 16.
7. Dichotomous Rasch model derived from specific objectivity, Wright BD, Linacre JM. … 1987, 1:1 p.5-6

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt21b.htm

Website: www.rasch.org/rmt/contents.htm