Rasch Model derived from Thurstone's Scaling Requirements

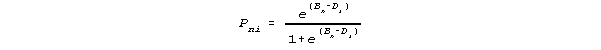
A popular "hierarchy" of psychometric models is

"1-parameter"

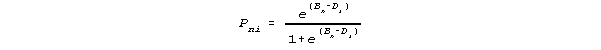
"2-parameter"

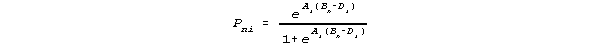
"3-parameter"

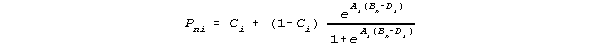
These models are said to be a "hierarchy" because when C_i = 0, then 3p becomes 2p, and when A_i=1, then 2p becomes 1p. This is sometimes interpreted to imply that the "best" model must be the one with the most parameters, i.e., 3p. The purpose of these models, however, is to construct scales on which measures can be made. The fundamental question, then, is do these models fulfill that purpose?

According to L.L. Thurstone (American Journal of Sociology, 1928, 33, 529-554, reprinted in The Measurement of Values, 1959, 228):

"The scale must transcend the group measured... One crucial experimental test must be applied to our method of measuring attitudes before it can be accepted as valid. A measuring instrument must not be seriously affected in its measuring function by the object of measurement. To the extent that its measuring function is so affected, the validity of the instrument is impaired or limited. If a yardstick measured differently because of the fact that it was a rug, a picture, or a piece of paper that was being measured, then to that extent the trustworthiness of that yardstick as a measuring device would be impaired. Within the range of objects for which the measuring instrument is intended, its function must be independent of the object of measurement."

What kind of model is necessary to meet Thurstone's requirement for a scale?

What model is required for the comparison and hence calibration of questions i and j to be independent of the persons used to elicit evidence of their relative standing on the scale? Questions i and j appear different only when they are answered differently. Realizing a comparison of i and j requires comparing how often i is answered "yes" when j is simultaneously answered "no" with how often the reverse happens.

1) The estimation of a comparison of i and j from these frequencies requires a comparison of their probabilities for some person n,

But this comparison must be the same regardless of which persons are involved. To satisfy Thurstone's requirement for scale validity, it must be the case that the comparison of questions i with j is always the same whoever the person.

2) Thus it must follow for any other person m that

3) For simplicity let j=o and m=o become the reference origins of the question and person scales so that the calibration of question i becomes its difference from "standard" item j=o and the measure of person n becomes its difference from "standard" person m=o, and align these scale origins so that P_mj = P_oo = ½, then

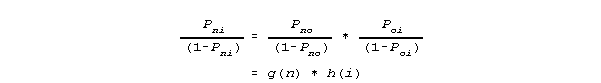
which defines a ratio scale for the measure of person n and the calibration of item i.

4) This ratio scale can be linearized by

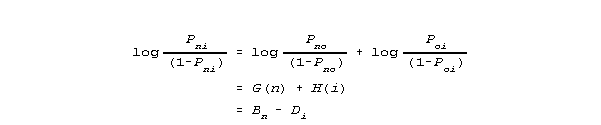
which when solved for P_ni shows that

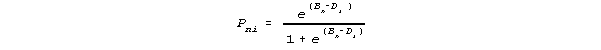
is the model necessary for Thurstone scale validity.

Step 2 can be rewritten to address Thurstone's concomitant 1926 requirement that the individual measure not depend on which particular items are used so that it becomes "possible to omit several test questions at different levels of the scale without affecting the individual score." This requires that the comparison of any pair of persons n and m be invariant with respect to the particular items employed as in

which is equivalent to step (2) and so leads to step (4).

Thus of the popular "hierarchy", only the "1-parameter" Rasch model meets Thurstone's requirement for scale validity. The "2-parameter" and "3-parameter" models do not. Their use does not, and cannot, produce a scale which is independent of the persons used to obtain it.

Benjamin D. Wright

Rasch model derived from Thurstone's scaling requirements. Wright B.D. … Rasch Measurement Transactions, 1988, 2:1 p. 13-4.

1. The Rasch Model derived from E. L. Thorndike's 1904 Criteria, Thorndike, E.L.; Linacre, J.M. … 2000, 14:3 p.763
2. Rasch model derived from consistent stochastic Guttman ordering, Roskam EE, Jansen PGW. … 6:3 p.232
3. Rasch model derived from Counts of Right and Wrong Answers, Wright BD. … 6:2 p.219
4. Rasch model derived from counting right answers: raw Scores as sufficient statistics, Wright BD. … 1989, 3:2 p.62
5. Rasch model derived from Thurstone's scaling requirements, Wright B.D. … 1988, 2:1 p. 13-4.
6. Rasch model derived from Campbell concatenation: additivity, interval scaling, Wright B.D. … 1988, 2:1 p. 16.
7. Dichotomous Rasch model derived from specific objectivity, Wright BD, Linacre JM. … 1987, 1:1 p.5-6

Please help with Standard Dataset 4: Andrich Rating Scale Model

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt21a.htm

Website: www.rasch.org/rmt/contents.htm