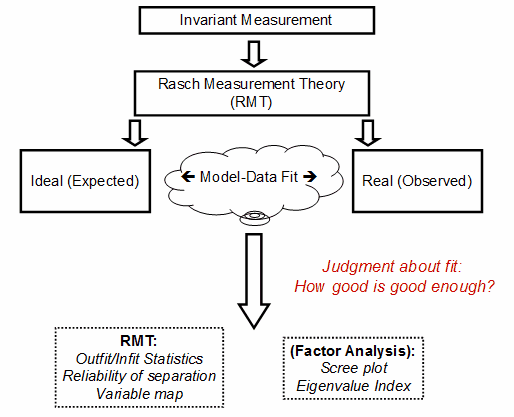
Figure 1. Conceptual Framework
The "Ask the Experts" series is a new feature in RMT in which experts throughout the world weigh-in on a number of controversial topics. For this issue, I have selected the topic of Rasch versus factor analysis. I selected this topic because numerous Rasch enthusiasts have mentioned many journal reviewers and editors continue to confuse the methodologies and sometimes require additional, and unnecessary, data analyses. Thus, the purpose of this piece is to provide readers with authoritative insights on Rasch versus factor analysis and help Rasch advocates overcome these common objections to Rasch analyses.
The expert panel for this piece includes Karl Bang Christensen from the Department of Biostatistics at the University of Copenhagen (Denmark), George Engelhard, Jr. from the Department of Educational Studies at Emory University (USA), and Thomas Salzberger from the Department of Marketing at WU Wien (Austria).
Exploratory factor analysis is a method for an entirely different situation, where no pre-specified hypothesis is tested. Furthermore, for a data set in, say, SPSS the user has to choose between seven options for 'extraction method', six options for 'rotation', and between covariance and correlation matrix. Even if a 'true model' exists there is little chance that choosing between these 84 different options yields a correct result.
Before deciding on Rasch analysis, confirmatory factor analysis, or a combination of the two, we need to consider the following: "what question do we want to answer?" We may outline different situations:
(i) We feel confident that items function well with regard to targeting, DIF and with nothing in the item content to suggest local dependence and the only unanswered question is dimensionality.
(ii) We feel less confident about the items, and want to study dimensionality along with evidence of local dependence, DIF and item fit.
(iii) In a given data set, we want to reduce a (possibly large) set of items to a small number of summary scale scores.
In situation (i) confirmatory factor analysis is adequate. Factor analysis based on polychoric correlations is likely to be at least as efficient as Rasch Analyses for disclosing multidimensionality. Larger correlations makes it more difficult to detect, but power of the tests increase with the sample size.
Situation (ii) is an example where confirmatory factor analysis alone is insufficient, mainly due to its inability to address spurious evidence (Kreiner & Christensen, 2011b). The Rasch model is the appropriate choice, possibly combined with confirmatory factor analysis.
Situation (iii) calls for Rasch analyses to be combined with exploratory and confirmatory factor analyses.
Unidimensionality is important and should be seen as one end of a continuum. Rather than asking 'unidimensional or not?', we should ask 'at what point on the continuum does multidimensionality threaten the interpretation of item and person estimates?' (Smith, 2002, p. 206). The Rasch literature is vague about this requirement and about recommendations as to its assessment (Smith, 1996). It is unreasonable to claim unidimensionality based solely on item fit statistics. However, unidimensionality is often assumed, rather than explicitly tested.
Infit and outfit test statistics summarizing squared standardized response residuals are widely used to test fit of data to the Rasch model, even though results concerning their distribution are based on heuristic arguments known to be wrong (Kreiner & Christensen, 2011a). When most items measure one dimension item fit statistics flag remaining items as misfitting. Item fit statistics are unlikely to have any power against multidimensionality, for dimensions with equal numbers of items, but patterns in residuals can indicate multidimensionality (Smith, 2002).
Response residuals should be interpreted with caution since their distribution is not known; however, indirect evidence shows when fitting unidimensional Rasch models to data where two underlying latent variables are responsible for the correlations, typically they result as negative correlation between residuals from items in different dimensions. However, no formal test is obtained. Importantly, evidence of local dependence should not automatically be interpreted as evidence of multi-dimensionality.
Formal tests can be obtained (e.g., the Martin-Löf test which is a likelihood ratio test statistic). Using a chi-square approximation will be useful only for disclosing multidimensionality in large samples when the correlation is modest (Christensen et al., 2002). Monte Carlo approaches that yield more powerful, but also time-consuming tests (Christensen & Kreiner, 2007) are also implemented.
The 't-test approach' tests equivalence of person estimates from two subsets of items (Smith, 2002), after converting the estimates to the same metric. The original approach compared estimates generated on subsets of items to estimates derived from the complete item set. However, in this situation the estimates are not independent (Tennant & Conaghan, 2007).
When the distribution of person location estimates is approximately normal a high proportion of persons with significantly different locations can be taken as evidence against unidimensionality, but since estimates of person locations for extreme scores are biased and non-normal, a cautious approach is recommended for skewed score distributions.
References
Christensen, KB, Bjorner JB, Kreiner S, & Petersen JH (2002). Testing Unidimensionality in Polytomous Rasch Models, Psychometrika, 67, 563-574.
Christensen, KB, & Kreiner, S (2007). A Monte Carlo Approach to Unidimensionality Testing in Polytomous Rasch Models, Applied Psychological Measurement, 3, 20-30.
Kreiner, S, & Christensen, KB (2011a). Exact Evaluation of Bias in Rasch Model Residuals. In Baswell (ed.) Advances in Mathematics Research, 12 (pp. 19-40).
Kreiner, S, & Christensen, KB (2011b). Item Screening in Graphical Loglinear Rasch Models. Psychometrika, 76, 228-256.
Rasch, G. (1960). Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen: Nielsen & Lydiche.
Rasch, G. (1961). On General Laws and the Meaning of Measurements in Psychology. Proceedings of the 4th Berkley Symposium on Mathematical Statistics and Probability, 4, 321-333. Reprinted in Bartholomew, D.J. (ed.) (2006) Measurement Volume I, 319-334. Sage Benchmarks in Social Research Methods, London: Sage Publications.
Smith E. (2002). Detecting and evaluating the impact of multidimensionality using item fit statistics and principal component analysis of residuals. Journal of Applied Measurement, 3(2), 205-231.
Smith, RM (1996). A comparison of methods for determining dimensionality in Rasch measurement, Structural Equation Modeling, 3, 25-40.
Tennant, A, & Conaghan, PG. (2007). The Rasch measurement model in rheumatology: What is it and why use it? When should it be applied, and what should one look for in a Rasch paper? Arthritis Care & Research, 57, 1358-1362.
Social, behavioral and health scientists increasingly use Rasch measurement theory (RMT) to develop measures for the key constructs included in their theories of human behavior (Engelhard, in press). As the number of research publications based on RMT increases, journal editors and peer reviewers who are unfamiliar with modern measurement theory may ask questions about the relationship between RMT and factor analysis (FA).
There are a variety of ways to view the relationships among RMT and FA. My perspective is represented in Figure 1. First of all, I view measurement through the philosophical lens of invariant measurement (IM). IM has been called "specific objectivity" by Rasch, and other measurement theorists have used other labels (Engelhard, 2008). The five requirements of IM are as follows:
Person measurement:
1. The measurement of persons must be independent of the particular items that happen to be used for the measuring:Item-invariant measurement of persons.
2. A more able person must always have a better chance of success on an item than a less able person: Non-crossing person response functions.
Item calibration:
3. The calibration of the items must be independent of the particular persons used for calibration: Person-invariant calibration of test items.
4. Any person must have a better chance of success on an easy item than on a more difficult item: Non-crossing item response functions.
Variable map:
5. Items and person must be simultaneously located on a single underlying latent variable: Variable map.
RMT can be viewed as a psychometric model that can meet the requirements of IM when there is acceptable model-data fit. In essence, RMT embodies ideal-type models that meet the requirements of IM. However, it is important to stress that with real data, IM reflects a set of hypotheses that are examined with a variety of model-data fit indices. As shown in Figure 1, I view the customary RMT indices of model-data fit (e.g., Outfit/Infit statistics, reliability of separation indices, and variable maps) as support for the inference that a particular data set has approximated the requirements of IM. Some of the analytic tools from FA can also be used to provide evidence regarding fit and unidimensionality, such as scree plots and eigenvalue-based indices Reckase (1979). Randall and Engelhard (2010) provide an illustration of using confirmatory FA and RMT to examine measurement invariance.
RMT and FA provide analytic tools for exploring model-data fit to explore hypotheses regarding invariant measurement. No single model-data fit index can detect all of the possible sources of misfit. Model-data fit is sample-dependent, and the key question in judging fit is: How good is good enough? There is no definitive statistical answer to this question, but various indices (including FA) can provide evidence to support inferences regarding invariance within a particular context.
 Figure 1. Conceptual Framework |
References
Engelhard, G. (in press). Invariant measurement: Using Rasch models in the social, behavioral, and health sciences. New York: Routledge.
Engelhard, G. (2008). Historical perspectives on invariant measurement: Guttman, Rasch, and Mokken [Focus article]. Measurement: Interdisciplinary Research and Perspectives (6), 1-35.
Rasch, G. (1960/1980). Probabilistic models for some intelligence and attainment tests. Copenhagen: Danish Institute for Educational Research. (Expanded edition, Chicago: University of Chicago Press, 1980).
Randall, J., & Engelhard, G. (2010). Using Confirmatory Factor Analysis and Rasch Measurement Theory to Assess Measurement Invariance in a High Stakes Reading Assessment. Applied Measurement in Education, 23, 286-306.
Reckase, M.D. (1979). Unifactor latent trait models applied to multifactor tests: Results and implications. Journal of Educational Statistics, 4, 207-230.
Striving for the same goal?
The Rasch model (RM) and factor analysis (FA) claim to serve the same purpose: measurement. This raises several questions. What is their relationship? Can we dispense with factor analysis altogether? Should Rasch analysis and factor analysis be carried out in a complementary fashion or side by side? There are no unambiguous answers to these questions; at least not if we take sociology of science into account.
RM and FA can be compared at the rather technical micro-level, which we will discuss later, or at the "philosophical" macro-level. At the latter, invariance as the defining property of the RM (Andrich 1988, 2010) is crucial. If invariance is empirically supported across samples from different subpopulations and occasions, in other words, across space and time, then measures are comparable and a uniform latent variable is a viable assumption within the established frame of reference. By contrast, if item parameter estimates fail to replicate across different samples or occasions, no common frame of reference can be established and the hypothesis of a uniform latent variable is untenable.
Multi-group FA (MG-FA) extends the idea of invariance to FA by imposing equality constraints mostly on factor loadings, item intercepts, and error variances (Meredith, 1993). This procedure has shortcomings, though. FA models do not separate respondent and item properties. Thus, factor loadings and item intercepts are sample dependent. It is therefore questionable whether truly invariant items will necessarily show invariance in MG-FA when respondent distributions and the targeting markedly differ. Furthermore, FA is associated with a series of highly problematic assumptions (see Wright 1996) with interval scale properties of item scores being probably the most serious (and generally deemed very unlikely) supposition. The point, though, is that if item scores are linear measures then FA is justified and the application of the RM is not. The reason for the latter is that the non-linear transformation of the raw score would be incorrect, since the raw score is already linear. Conversely, if the item scores are non-linear, the application of FA is unjustified (see Waugh and Chapman, 2005), while the RM is appropriate. This implies that the RM and FA are, strictly speaking, incompatible, mutually exclusive models. While the RM, by assessing fit, investigates whether observed person raw scores can be converted into linear person measures and observed item raw scores into linear item measures, FA requires measures as the input.
Misfit of the data to the RM implies that item scores are not even ordinal or non-linear (Salzberger, 2010), but merely numerals arbitrarily assigned to response options. Ironically, this is what proponents of Stevens' (1946, 1951) definition of measurement mistake for constituting measurement and what represents a factor analyst's only "evidence" of measurement at the item level. In other words, FA requires what it purports to provide: measures. If one rejects Stevens' definition of measurement and deems invariance a necessary requirement of measurement, there is, in fact, no point in applying FA in addition to the RM.
 Figure 2. Sample CFA and Rasch Output |
A pragmatic perspective
From a more pragmatic point of view, one might argue that even though the FA of non-linear scores is, strictly speaking, wrong, FA, specifically exploratory FA, may provide insights that inform a subsequent Rasch analysis. In a simulation study, Smith (1996) found that FA outperforms Rasch fit analysis in the assessment of unidimensionality in a two-factor model, when the correlation between the factors is small (<0.30) and the number of items per dimension balanced. By contrast, with higher correlations and uneven numbers of items, the fit statistics in the Rasch analysis are more powerful. Thus, from a technical point of view FA could be used prior to a Rasch analysis as a tool to generate hypotheses of separate unidimensional variables. Having said that, proper scale development and analysis should never be confined to a statistical procedure (even if that procedure utilizes the RM), but should be guided by a theory of the construct to be measured. It is hard to imagine how the existence of two hardly related dimensions can go unnoticed in previous qualitative work. Moreover, the diagnostic techniques tailored to unidimensionality have been refined since Smith's study. In particular, the principal component analysis on the item residuals (Linacre 1998, available, for example, in RUMM 2030, Andrich et al., 2012 or Winsteps, Linacre, 2012) or the g-detect procedure (Kreiner and Christensen, 2004, available in DIGRAM, Kreiner, 2003) offer powerful approaches to investigate dimensionality. Today, there does not seem to be any need for conducting a FA on the raw data prior to a Rasch analysis. In fact, researchers might feel the need to run a confirmatory FA (CFA) after the Rasch assessment of a scale in order to use measures in a structural equation model (SEM). However, Rasch measures can be integrated into SEM quite easily. Instructions how to do this can be found in Salzberger (2011).
The sociology of science perspective
From a Rasch perspective, there is no need to run a FA prior to, simultaneously with, or after a Rasch analysis. On the other hand, anyone who has ever tried to publish a Rasch analysis of a scale will have very likely been confronted with the problem of explaining the differences between the RM and FA, felt the pressure to justify the use of the RM, and probably also experienced resistance and refusal. This is where the sociology of science comes in. When one gets into a dispute between paradigms (Andrich 2004), there are at least three different strategies we could pursue, which we might want to call the pure approach, the comparative approach, and the assimilation strategy. First, following the pure approach, the researcher compares the RM and FA at the theoretical macro-level stressing the unique properties of the RM and its relationship to the problem of measurement. The empirical analysis is confined to the RM. Second, the comparative approach aims at exposing empirically the differences between the RM and FA. The RM and FA can be compared at the macro-level, but also at the micro-level. The latter describes, for example, which parameters in the RM correspond most closely to parameters in FA (see Wright, 1996; Ewing et al., 2005). Third, in the assimilation strategy, the Rasch analysis and FA are forced to converge, or at least presented in a way that suggests comparable results based on the RM and FA. Since this strategy downplays the theoretical differences between the RM and FA, a comparison focuses on the micro-level.
The pure approach is probably the most consistent and meaningful path but also the most confrontational. The comparative approach may provide interesting insights but raises the problem of how to argue the superiority of the RM over FA to an audience that does not acknowledge the theoretical underpinnings of the RM. There is a serious threat of falling into the trap of trying to empirically decide whether the RM or FA is better. The assimilation strategy can actually be detrimental to the dissemination of the RM as it easily creates the impression that the RM and FA lead eventually to the same or very similar results. The assimilation strategy can also be pursued unwittingly, particularly when existing scales, originally developed based on FA, are reanalyzed using the RM. Such scales often show a limited variation in terms of item locations. Then the RM as well as FA might exhibit acceptable fit. In addition, the correlation between factor scores, or raw scores, and Rasch measures are typically very high leading to the false impression that the application of the RM generally makes no substantial difference. Issues like invariance, the construct map, the interpretation of measures with reference to items, or targeting, to name just a few, are suppressed.
Conclusions
A Rasch analysis, in principle, hardly benefits from additional input from FA. However, in the interest of acceptance, researchers might feel pressed to incorporate FA into a Rasch paper. Combining Rasch analysis with FA increases the likelihood that non-Rasch researchers (specifically reviewers and editors) become connected with a Rasch paper and that Rasch measurement appears less menacing. At the same time researchers should be cognizant of the potential for misrepresenting the differences between the RM and FA. In any case, it is pivotal to outline the requirements of measurement and to ensure that the Rasch philosophy and the theory of the construct guide the scale development and formation. Then the complementary presentation of results based on FA makes no difference to substantive conclusions. Contributions that aim at a methodological comparison of Rasch measurement and FA are, of course, a different issue.
References
Andrich, D. (1988). Rasch models for measurement. Beverly Hills: Sage Publications.
Andrich, D. (2004). Controversy and the Rasch model: a characteristic of incompatible paradigms? Medical Care, 42, 1-16.
Andrich, D. (2010). Sufficiency and conditional estimation of person parameters in the polytomous Rasch model, Psychometrika, 75(2), 292-308.
Andrich, D., Sheridan, B.S., & Luo, G. (2012). Rumm 2030: Rasch Unidimensional Measurement Models (software). RUMM Laboratory Perth, Western Australia.
Ewing, M.; Salzberger, T., & Sinkovics, R. (2005). An Alternate Approach to Assessing Cross-Cultural Measurement Equivalence in Advertising Research. Journal of Advertising, 34(1), 17-36.
Kreiner, S. (2003). Introduction to DIGRAM [computer software], Department of Biostatistics, University of Copenhagen (www.biostat.ku.dk).
Kreiner, S., & Christensen, K.B. (2004). Analysis of Local Dependence and Multi-dimensionality in Graphical Loglinear Rasch Models, Communications in Statistics - Theory and Methods, 33, 1239-1276.
Linacre, J.M. (1998). Structure in Rasch residuals: Why principal components analysis (PCA)? Rasch Measurement Transactions, 12(2), 636.
Linacre, J.M. (2012). Winsteps 3.75, [Rasch Model Computer Program], Chicago, Il, 1991-2012.
Meredith, W. (1993). Measurement invariance, factor analysis and factorial invariance, Psychometrika, 58 (4), 525-543.
Salzberger, T. (2010). Does the Rasch Model Convert an Ordinal Scale into an Interval Scale? Rasch Measurement Transactions, 24(2), 1273-75.
Salzberger, T. (2011). Specification of Rasch-based Measures in Structural Equation Modelling (SEM). Available from: www2.wu.ac.at/marketing/mbc/download/Rasch_SEM.pdf.
Smith, R, (1996). A Comparison of Methods for Determining Dimensionality in Rasch Measurement. Structural Equation Modeling - A Multidisciplinary Journal, 3(1), 25-40.
Stevens, S.S. (1946). On the Theory of Scales of Measurement, Science, 103, 667-680.
Stevens, S.S. (1951). Mathematics, Measurement, and Psychophysics. In S.S. Stevens (ed), Handbook of Experimental Psychology, New York, NY: Wiley, pp. 1-49.
Waugh, R.F., & Chapman, E.S. (2005). An Analysis of Dimensionality Using Factor Analysis (True-Score Theory) and Rasch Measurement: What Is the Difference? Which Methods is Better? Journal of Applied Measurement, 6 (1), 80-99.
Wright, B. (1996). Comparing Rasch Measurement and Factor Analysis. Structural Equation Modeling - A Multidisciplinary Journal, 3(1), 3-24.
For more information,
The Impact of Rasch Item Difficulty on Confirmatory Factor Analysis , S.V. Aryadoust … Rasch Measurement Transactions, 2009, 23:2 p. 1207
Confirmatory factor analysis vs. Rasch approaches: Differences and Measurement Implications, M.T. Ewing, T. Salzberger, R.R. Sinkovics … Rasch Measurement Transactions, 2009, 23:1 p. 1194-5
Conventional factor analysis vs. Rasch residual factor analysis, Wright, B.D. … 2000, 14:2 p. 753.
Rasch Analysis First or Factor Analysis First? Linacre J.M. … 1998, 11:4 p. 603.
Factor analysis and Rasch analysis, Schumacker RE, Linacre JM. … 1996, 9:4 p.470
Too many factors in Factor Analysis? Bond TG. … 1994, 8:1 p.347
Comparing factor analysis and Rasch measurement, Wright BD. … 1994, 8:1 p.350
Factor analysis vs. Rasch analysis of items, Wright BD. … 5:1 p.134
Ask the Experts: Rasch vs. Factor Analysis. Karl Bang Christensen, George Engelhard, Jr., Thomas Salzberger ... Rasch Measurement Transactions, 2012, 26:3 p. 1373-8
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt263a.htm
Website: www.rasch.org/rmt/contents.htm