Reliability, Separation and Strata: Percentage of Sample in Each Level

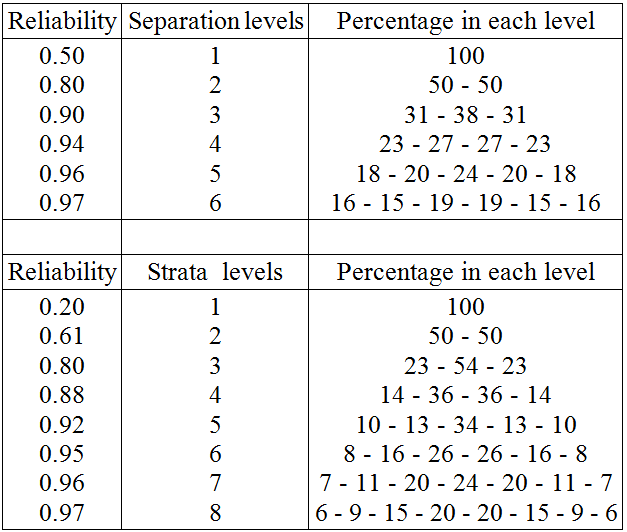
Test Reliability (Person Reliability) is routinely reported when analyzing responses to a test. It is the true variance of the sample of test respondents divided by their observed variance, where observed variance = true variance + error variance, and similarly Item Reliability can be reported for the sample of test items. Reliabilities are in the range 0 - 1, but when their values exceed 0.9, the practical implications of increases in Reliability become obscured by the range restriction toward 1.0. This motivated a transformation of Reliability into Separation, where Separation = square-root (true variance / error variance). Separation reports how many statistically distinguishable measurement levels exist in the sample when very high and very low measures are modeled to be accidental. A refinement of Separation is Strata, where Strata = (4 * Separation + 1) / 3. Strata models the very high and very low measures to be additional levels of performance.

For approximately normally-distributed samples, a rough estimate of the percentage of the sample in each Separation or Strata level can be computed. Levels are defined to be 3 errors apart. This distance slightly exceeds statistical significance at p = .05. The percentages in each level are shown in the Table.

John Michael Linacre

Wright BD. (1996). Reliability and separation. Rasch Measurement Transactions, 9(4), p. 472. Available at: www.rasch.org/rmt/rmt94n.htm

Wright BD, Masters GN. (2006). Number of Person or Item Strata: (4*Separation + 1)/3. Rasch Measurement Transactions, 16(3), p. 888. Available at: www.rasch.org/rmt/rmt163f.htm

Reliability, Separation and Strata: Percentage of Sample in Each Level. John M. Linacre … Rasch Measurement Transactions, 2013, 26:4 p. 1399

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt264g.htm

Website: www.rasch.org/rmt/contents.htm