Number of Person or Item Strata: (4*Separation + 1)/3

Wright and Masters (Rating Scale Analysis, 1982, pp. 92, 106) write: "... if we define statistically distinct levels of item difficulty as difficulty strata with centers three calibration errors apart, then this separation index G can be translated into the number of item strata defined by the test H=..." (emphasis mine) and similarly for persons.

H = (4G + 1)/3

where G = Separation index = "True" standard deviation / Average measurement error

Note: in RUMM2020 documentation, the "Separation Index" is the reliability = G² / (1+G²).
David Andrich (1982) An Index of Person Separation in Latent Trait Theory, the Traditional KR-20 Index, and the Guttman Scale Response Pattern. Education Research and Perspectives, 9:1, 95-104.

The "average measurement error" is the statistical average, i.e., the root-mean-square, of the standard errors of the measures of items of persons. The "True" standard deviation of the item or person measures is obtained from:

"True" standard deviation² = Observed standard deviation² - average measurement error².

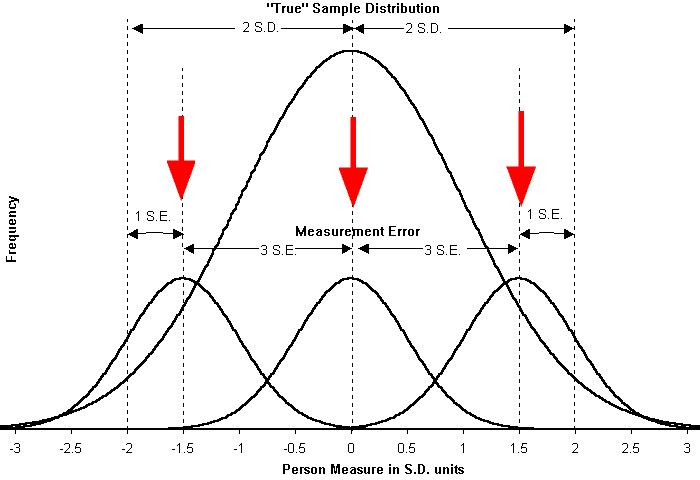
What does this mean? The plot shows the relationship between sample distribution and measurement error when H=3, i.e., when 3 strata are observed. This is when G=2, so that the "true" sample standard deviation, S.D., is twice the average measurement error, S.E. We see that the relevant range of the "true" distribution (assumed normal) is two standard deviations away from the mean, encompassing over 95% of the distribution. Compare this plot with the "Separation" plot in RMT 9:4.

H=3 Three Statistical Strata

Imagine that Person 1 is in the middle of strata 1 at location A with S.E. sized S. Person 2 is in the middle of strata 2 at location B with S.E. also sized S. The S.E.s are assumed the same for convenience (as in CTT). So their distance apart is (A-B) with S.E. sqrt(2)*S. The 2-sided 95% confidence interval for the distance (A-B) is 1.96*sqrt(2)*S = 2.77*S, so this is the distance between the middles of the strata.

The strata are defined as statistically distinct measures. In the "true" distribution, they are located 3 S.E. apart, because this is conveniently more than 1.96 * sqrt(2) = 2.77 S.E., the distance corresponding to .05 significance. The centers of the extreme strata are also positioned 1 S.E. within the boundaries of the sample distribution. Thus 84% of even the most extreme strata lie within the 4 S.D. range. In the observed distribution, the strata are located 3*S.E.*Observed S.D./True S.D. apart. The extreme strata are narrower. The strata are symmetric around the Observed mean.

G itself is a more conservative "Separation Index" than H. For instance, suppose that the "true" standard deviation of a sample is the same as the average measurement error. Then G=1, and the test reliability is 0.5, warning us that we don't know whether observed differences within the sample are real differences or merely measurement error. H is (4+1)/3, i.e., roughly 2. This indicates that the opposite ends of the "true" distribution are measurably different, implying that, if the observed measures are sufficiently far apart, they probably reflect real differences.

Number of Person or Item Strata: (4*Separation + 1)/3. Wright BD, Masters GN. … 2002, 16:3 p.888

Notes:

1. In practice, for G < 3.5, H = G+1. For G >= 3.5, H = G+2.
2. Ben Wright preferred to use G as the count of strata, rather than H, in classroom teaching.
3. For G and H, the levels are 3 S.E.s apart, centered on the sample mean.
4. For H, the levels in the true distribution are 12*"True S.D."/(3H - 1) apart, centered on the sample mean.
   For H, the levels in the observed distribution are 12*"Observed S.D."/(3H - 1) apart, centered on the sample mean.
5. For G, the levels in the true distribution are 3*"True S.D."/G apart, centered on the sample mean.
   For G, the levels in the observed distribution are 3*"Observed S.D."/G apart, centered on the sample mean.

1. Reliability, separation, strata statistics, Fisher WP Jr. … 6:3 p.238
2. Reliability and separation nomograms, Linacre JM. … 1995, 9:2 p.421
3. Reliability and separation, Wright BD. … 1996, 9:4 p.472
4. Predicting Reliabilities and Separations of Different Length Tests, Linacre, J.M. … 2000, 14:3 p.767
5. Going beyond Unreliable Reliabilities, Mallinson T., Stelmack J. … 2001, 14:4 p.787-8
6. Separation, Reliability and Skewed Distributions: Statistically Different Levels of Performance, Wright B.D. … 2001, 14:4 p.786
7. Number of Person or Item Strata (4G+1)/3, Wright BD, Masters GN. … 2002, 16:3 p.888
8. Cash value of Reliability, WP Fisher … Rasch Measurement Transactions, 2008, 22:1 p. 1160

Number of Person or Item Strata. Wright BD, Masters GN. … Rasch Measurement Transactions, 2002, 16:3 p.888

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt163f.htm

Website: www.rasch.org/rmt/contents.htm