David Andrich
The University of Western Australia
In analyses of test data according to traditional classical test theory (CTT), the emphasis is on item and sample statistics calculated in terms of raw scores, and perhaps the best known of these statistics is the KR-20 index of internal consistency. In contrast, the emphasis in latent trait theory is on item and person parameter estimates, which are nonlinear transformations of raw scores, and on variances of these estimates. Using this emphasis of latent trait theory in Rasch's simple logistic model, it is shown through a series of simulations that the observed variance among the person parameter estimates and variances of these estimates for each person can be used to construct an index which gives values virtually identical to the KR-20 index. Implications of this result are discussed, particularly with respect to the evaluation of the degree to which an observed pattern of responses conforms to the scaling criterion of Guttman.
Relatively recently, some steps have been taken to articulate and reconcile various relationships among indices of internal consistency obtained from traditional test theory (Terwilliger and Lele, 1979; Cudeck, 1980). In some cases these analyses have also incorporated concepts of latent trait theory (Cliff, 1977). The most popular index of internal consistency, and the one used as a baseline for the consideration of others, is the Kuder-Richardson 20 formula for dichotomously scored items (Kuder and Richardson, 1937) and its generalization, coefficient alpha (Cronbach, 1951). The emphasis in this paper is on dichotomously scored achievement items and therefore on the KR-20 formula.
The idea of internal consistency is that items of a test all reflect the `same thing'. The `same thing' in this sense, as explicated by Cronbach (1951) and Lumsden (1957) does not necessarily mean a single `pure' factor or characteristic. Each item may involve a combination of more `pure' characteristics, but if all the items have these different characteristics represented in them in the same proportions, then the test will appear to be internally consistent. The counterpart of the idea of internal consistency in latent trait theory is the idea of unidimensionality, that is, that a person may be represented by a single value on a single latent continuum. Unidimensionality in latent trait theory, as internal consistency in traditional test theory, is a relative and not an absolute matter. Operationally, the Guttman scale (Guttman, 1950) is seen as the ideal in terms of evidence of unidimensionality. Its connection with traditional theory notions of internal consistency is that the closer the responses conform to this ideal, the greater the value of the KR-20 index.
The ideal of a Guttman scale is difficult to achieve in real testing, the main obstacle being the requirements that the responses of a person to an item be governed in a determinate way. Therefore, the realization of a Guttman scale is enhanced if items have a large spread in difficulty, and if no two items are close together on the scale. It helps also if the range of abilities of persons is relatively large, preferably covering the wide range of item difficulties. The degree to which a set of responses conforms to a Guttman scale can be indicated from various indices of reproducibility (Guttman, 1947).
The probabilistic counterpart of the ideal of the Guttman response pattern is the simple logistic model (SLM) of Rasch. Although this relationship has been broached in the literature (Brink, 1972; Andrich, 1981), it seems not appreciated as generally as it might be. In developing the SLM, Rasch (1960, 1980: 66) in fact presents a pattern of ideal results for ordering persons and items which take the Guttman form. The responses of persons to items which conform to the SLM, conform to the Guttman scale in terms of probabilities. That is, if one orders the items in terms of difficulties and persons in terms of abilities, then the actual probabilities of a correct response, which are themselves determinate, follow a strict ordering. Consistent with the SLM's being a probabilistic counterpart of the Guttman scale, if item difficulties are spread greatly, then responses generated according to the SLM will reveal a Guttman pattern. In other words, the deterministic Guttman pattern of responses is a limiting case of the probabilistic SLM pattern.
When studying response patterns with respect to the SLM criterion or its limiting case, the Guttman pattern, it is difficult to avoid attending to the fact that the criterion is required as much for the response patterns of persons as it is of items. In contrast, in traditional test theory and in the construction of the KR-20 index, the focus tends to be on the statistics of the items, and any consideration of the response patterns of the persons tends to be only incidental. With respect to any effect on the KR-20, the only feature of the responses of the persons which is noted is the variance of the total scores of persons; this is noted because in general, the greater the variance of the total scores of persons, the greater the value of the KR-20 index. However, as Cliff (1977) points out, `consistency of person ordering would appear to be more relevant to the purpose of testing than consistency of item ordering, the former being the primary goal of testing' (385).
This paper explores the information available from the KR-20 index, but from the point of view of latent trait theory. More specifically, the emphasis is on person measurement using the SLM, and on an index which has numerical values virtually identical to that of the KR-20 index. After a brief explanation of the index, a small simulation study is used to demonstrate the closeness of the values of the two indices.
The Simple Logistic Model and Person Measurement
There are a number of complementary reasons for choosing the SLM rather than the other latent trait models (Birnbaum, 1968), and then for focussing on person measurement rather than on item statistics. With respect to the latter point, in all latent trait theory the emphasis is on the advantages that accrue from having an estimate of a person parameter and on having a standard error for this estimate. It seems appropriate therefore to consider these same features when attempting to make connections on perspectives of traditional test theory. By focussing on person measurement in the latent trait framework it is more likely that new insights can be gained than by focussing on item statistics which form the cornerstone of the traditional test theory.
One reason for choosing the SLM has already been broached, namely, that it is a probabilistic counterpart of the Guttman scale which itself is considered an ideal with respect to unidimensionality. The second related reason is that it is the only latent trait model where the total score of a person on a test is sufficient to estimate a person's ability and the total score of an item is sufficient to estimate its difficulty. This makes it parallel the traditional test theory circumstances, in which these statistics are used directly for a person's ability estimate and an item's difficulty estimate respectively, more closely.
Since Rasch (1960, 1980) published his monograph Probabilistic models for some intelligence and attainment tests, many publications (e.g. Wright & Panchapakesan, 1969, Wright & Douglas, 1977; Spada & Kempf, 1977; Gustafsson, 1977), have appeared which discuss the formulation, properties, and related empirical results of the simple logistic model. Therefore only a summary of equations necessary for the particular development and for completeness will be presented here.
If βv is the ability of person v, δi the difficulty of item i, and xvi is a Bernoulli random variable which takes the value xvi = 1 for a correct response and 0 otherwise, then the probability Pxvi of the response xvi is given by:
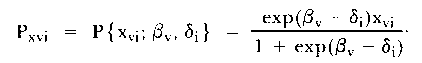
| (1) |
From the available responses the usual task is to estimate these parameters. A number of estimating algorithms, more or less complicated and practical (e.g. Rasch, 1960; Andersen, 1973; Allerup and Sorber, 1977; Wright and Panchapakesan, 1969) have been devised. The one considered here is documented by Wright and Douglas (1977). Called the unconditional maximum likelihood (JMLE) approach, it is relatively simple to apply routinely on a computer, and is based on maximizing the likelihood of the matrix of responses of N subjects to K items. The resultant equations to be solved simultaneously are:
| si = Σv P^vi, i = 1,...,K; | (2) |
| rv = Σi P^vi, v = 1,...,N; | (3) |
| and Σi δ^i = 0. | (4) |
where si = Σv xvi is the total score of item i, rv = Σi xvi is the total score of person v, and
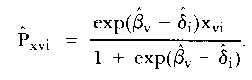
|
Because the estimates of δi from the above equations are [biased], the estimates obtained from (2) are multiplied by the factor (K - 1)/K, and the βv re-estimated from (3).
Associated with the item and person parameters are the asymptotic estimates of their variances; these are approximated respectively by:
| σ^i² ~= 1 / Σv P^vi (1 -P^vi ) | (5) |
| and σ^v² ~= 1 / Σi P^vi (1 -P^vi ) | (6) |
An Index of Person Separation
Suppose that the estimated ability βv is resolved according to
| β^v = βv + εv | (7) |
where εv is the error of the estimate, or error of measurement, for person v. Then
| E[β^v; βv] = βv] | (8) |
| and V[β^v; βv] = Vεv; βv] = σε² . | (9) |
For any given person, σv² of equation (6) estimates σε² which is assumed to be associated with person v selected from a population. Suppose that this population has mean μ and variance σβ² and let
| βv = μ + φv | (10) |
where φv indicates the deviation of person v from the population mean.
| E[β] = μ | (11) |
| and V[β] = V[φ] = σβ² | (12) |
Substituting (10) into (7) gives
| β^v = μ + φv + εv | (13) |
| E[β^] = μ | (14) |
and, on the assumption that βv and εv are uncorrelated in the population,
| V[β^] = σβ^² = σβ² + σε² . | (15) |
Thus an expression for the variance of actual abilities is simply
| σβ² = σβ^² - σε² . | (16) |
By considering the variance among the estimates of persons tested in some group relative to the error variance for each person, an index indicating how reliably the persons are separated can be constructed in the usual way as a ratio of true variance to observed variance. Denoting the index by rβ and calling it an index of person separation to distinguish it from other similar indices of reliability, it may be expressed as
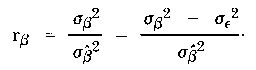
| (17) |
[Note: Wright's Separation Index (formulated later than Andrich's) is σβ / σε = √ ( rβ / (1 - rβ ))]
An estimate σ^β^² of σβ^² aa2 can clearly be obtained from Σv (β^v - β- ^v )² / (N - 1), and on the assumption that σ^v² is homogeneous among persons, which is not strictly correct since in general σ^v² varies with β^v, the average of the estimated within person variances σ^v² given by Σv σ^v² / N provides an estimate of σεy².
For completeness, it is noted that the KR-20 formula may be expressed as
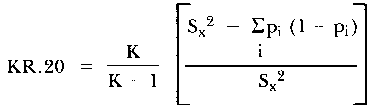
| (18) |
where Sx² is the variance of the total scores of the persons and pi is the proportion of persons passing item i. Clearly, the index rβ has the structure of KR-20, but whereas the latter index is expressed in terms of both the variance among persons through the term Sx² and the variance of items through the term Σi pi (1 - pi), the former index is expressed entirely in terms of parameters associated with persons.
The idea of an index such as rβ defined above is a natural one and has been broached indirectly by Bock (1972), who considered it more appropriate for traditional test theory and saw little use for it in latent trait theory, and by Lumsden (1978) who, after noting its possible construction, rejected it as having no worthwhile function. The main reason for the view that this index is unnecessary in latent trait theory is that in this theory the emphasis is on the explicit tests of fit of responses to the model and on standard errors of the estimates of the parameters.
Andrich and Douglas (1977), who derive the index in the same way as developed above, point out that there are circumstances when the researcher needs to know, not only how a set of items conforms to a unidimensional structure, but also how reliably the persons measured are separated. This occurs, for example, if the parameter estimates obtained for a set of persons are to be entered subsequently into a regression equation as values of either a dependent or explanatory variable.
Whether the test is evaluated from either a traditional or a latent trait theory point of view, it is important to know in such a case that the variation among the estimated person parameters is not simply error variance. However, the index is used here for the purpose of making a connection between person parameters from a latent trait model and an index of internal consistency based on item statistics derived from traditional test theory, and not on its possible uses.
The demonstration of the closeness of the values of rβ and KR-20 is shown in the following small simulation study.
The Simulation Study
All simulations in this study involved responses which conformed to the SLM. Because the KR-20 index varies as a function of the number of items, the range of item difficulties, and the variance of the scores of the persons, all three factors were varied. However, they were not varied independently, as is described below. The number of items in the tests ranged from 9 to 48, and the difficulties of the items in each set were uniformly distributed with a mean of zero.
For each given number of items in a test, five or more distributions of person abilities, each with a mean of zero, but with standard deviations ranging between σβ = 0 and σβ = 2.0, were generated. Except in the distribution where σβ = 0, distributions were normal. For each fixed number of items in a test, the range of item difficulties was varied to parallel the standard deviations of the person abilities; the greater σβ the greater the range of item difficulties. To some degree, this relationship represents the real situation where attempts are made generally to center the item difficulties on the hypothesized abilities of the persons, and to match the range of abilities with the range of item difficulties. The set-up of the simulations and the corresponding values of the KR-20 and the rβ indices are shown in Table I.
|
TABLE I Comparison of Two Indices from Data Sets Simulated according to the Simple Logistic Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| Number of Items | 0.0 0.0 | 0.25 0.80 | 0.50 1.6 | 0.75 2.50 | 1.0 3.0 | 1.5 4.0 | 2.0 5.0 | Population Standard Deviation Item Difficulty Range |
| 9 | .04, .13 -.09 | .11, .17 -.06 | .26, .30 -.04 | .42, .42 .00 | .46, .46 .00 | (KR^-20,
r^β) (KR^-20 - r^β) | ||
| 12 | .02, .12 -.10 | .18, .26 -.08 | .44, .46 -.02 | .57, .58 -.01 | .62, .61 .01 | |||
| 19 | .01, .08 -.07 | .09, .17 -.08 | .52, .53 -.01 | .61, .63 -.02 | .62, .64 -.02 | .82, .79 .03 | .84, .82 .02 | |
| 21 | -.13, -.06 -.07 | .28, .32 -.04 | .51, .53 -.02 | .70, .71 -.01 | .78, .77 .01 | .87, .85 .02 | .89, .87 .02 | |
| 27 | .55, .53 .02 | .73, .74 -.01 | .84, .83 .01 | .89, .88 .01 | .92, .91 .01 | |||
| 36 | .60, .60 .00 | .82, .81 .01 | .85, .84 .01 | .91, .90 .01 | .95, .93 .02 | |||
| 48 | .71, .72 -.01 | .85, .84 .01 | .89, .89 .00 | .94, .93 .01 | .96, .95 .01 | |||
The values for KR-20 and rβ indices are very similar, with a trend evident in the table. This trend shows that with small numbers of items and small range of abilities, the value of rβ is slightly greater than the value of KR-20. This can be explained by noting first that the non-linear transformation of raw scores to abilities according to equation (3) `stretches' the extreme raw scores more than the central scores, and secondly, that with a small number of items and narrow range of difficulties, a relatively great number of persons have the extreme scores. The opposite holds for cases where distributions of person abilities and item difficulties are greater. However, even so, the greatest difference between rβ and KR. 20 is 0.10, and this is in the somewhat unrealistic extreme situation where both the standard deviation of person abilities and the range of item difficulties is zero. In the cases where these indices are more meaningful, the values are much closer. For example, of the 25 cases where KR-20 > 0.50, the maximum difference of 0.03 occurred once, while differences of 0.02 or less occurred the other 24 times.
Discussion and Conclusions
The most obvious feature of the results of Table I is the closeness of the values of the rβ and KR-20 indices. In some ways, therefore, the index rβ is redundant. However, as stressed throughout the paper, it is derived in terms of a latent trait model, and with a focus on measurement of persons and not on the statistics of items. An associated advantage with its definition in terms of variation among persons relative to the error of estimate for each person is that it is consistent with the intuitive notion of the traditional reliability of a test, namely, how reliably does it distinguish among the test-takers. In addition, focussing on the quality of the separation of persons makes it clear that the index is not a property simply of the test, but a property of the test in relation to the persons tested. From a latent trait perspective, this is as expected because the standard error of measurement is a function of the number of items and of the relationship of the difficulties of the items to the abilities of the persons.
This emphasis on the measurement of persons is also consistent with the point made by Cliff (1977) in his explorations of indices of consistency and his recognition of '... the duality of person and item relations', and that `Surely we are not interested in consistency of item ordering per se, but rather in consistency and completeness of person ordering' (393). In relation to this important issue of person ordering, the SLM is the most appropriate latent trait model because it captures the characteristics of ordering of persons in terms of their unweighted total scores. This makes it consistent with the ideal Guttman scale and its requirement that the total score of a person be sufficient to recover the pattern of responses, though as pointed out earlier, through a probabilistic rather than a deterministic pattern model.
Although the details are beyond the scope of this paper, it is relevant to note that the rβ and KR-20 indices give values as similar as those shown in Table I even when data do not in fact conform to the SLM and with as great a variation in values. Thus data can conform to the SLM, and have a range of rβ or KR-20 values effectively from 0 to 1, or they may not conform to the SLM and still have the same effective range of rβ or KR-20 values.
To appreciate the implication of these possibilities, consider first the case where the data do conform to the SLM. Then the greater the variation in the item difficulties and person abilities, the greater the opportunity for the ordering of persons to reveal itself. In the limit of this variation and as rβ -> 1, the ideal Guttman scale is produced. In the other extreme in which the variations in item difficulties and person abilities tend to zero, rβ -> 0 and the response patterns show no ordering. Any differences among observed responses are random. The value rβ = 0 provides evidence that the differences among ability estimates of persons, and therefore among any order that may be observed, are no greater than would be expected by chance relative to the error of measurement.
Second, consider the case where the data do not conform to the SLM, but all items reflect to a greater or lesser amount the same latent trait. Then once again, for a given degree of non-conformity to the SLM, the greater the variation in item difficulties and person abilities, the greater the value of ro and the closer the observed pattern of responses conforms to the Guttman ideal. But to the degree that the responses do not conform to the SLM, to that degree the rate at which the Guttman ideal is approached as rβ -> 1 is reduced. The implication of these two conditions is that the better the responses conform to the SLM and the greater the value of rβ, then the closer the observed responses will reflect the Guttman pattern. These would seem to be better and easier criteria to apply than some of the reproducibility indices generally associated with analyses of responses from the perspective of the Guttman scale.
Gustafsson (1980) provides a comprehensive summary of techniques for testing the fit of responses to the SLM, though most papers dealing with the model include discussions of tests of fit. With respect to a Guttman scale, the index ro provides complementary information to these techniques.
Three further points in relation to the rβ index and the SLM may be worth making. Firstly, incomplete data pose no problems in computing this index. Algorithms for estimating parameters with incomplete data are readily available with the SLM (Choppin, 1980). The consequence of incomplete data is that the standard errors of estimates are increased with an increase in missing responses, and as a result the index rβ will clearly decrease.
Secondly, it should be stressed that the derivation of rβ as shown in equation (17), and the values of σβ and σε used in this equation, contrasts in an important way with the derivation of KR-20. This is that σβ and σε are derived from non-linear transformations of observed scores while the KR-20 index is derived in terms of observed scores. Therefore, the virtual identity of the calculated rβ and KR-20 values in the various data sets provides an interesting algebraic problem, namely, how to demonstrate explicitly the approximate equality of these two indices.
Finally, having the facility to capture the most well known and commonly used index of traditional test theory; to provide evidence of the degree of conformity of a set of responses to a Guttman scale in a probabilistic sense with the limiting case indicating a perfect Guttman pattern; and to provide these from a latent trait formulation, indicates that Rasch's simple logistic model provides an extremely parsimonious perspective from which to evaluate test data.
An Index of Person Separation in Latent Trait Theory, the Traditional KR-20 Index, and the Guttman Scale Response Pattern, David Andrich
Education Research and Perspectives, 9:1, 1982, 95-104.
REFERENCES
Allerup, P. & G. Sorber, The Rasch model for questionnaires with a computer program. Copenhagen, The Danish Institute for Educational Research, 1977, 4.
Andersen, E. B., A goodness to fit test for the Rasch model. Psychometrika, 1973, 38, 123-90.
Andrich, D., Rasch's models and Guttman's principles for scaling attitudes. Paper presented at a conference in Honour of Georg Rasch, Chicago, Illinois, 1981.
Andrich, D. & G. A. Douglas, Reliability: Distinctions between item consistency and subject separation with the simple logistic model. Paper presented at the Annual Meeting of the American Educational Research Association, New York, 1977.
Birnbaum, A., Some latent trait models and their use in inferring an examinee's ability. In F. M. Lord & M. R. Novick (eds), Statistical theories of mental test scores. New York, Addison-Wesley, 1968.
Bock, R. D., Estimating item parameters and latent ability when response are scored in two or more nominal categories, Psychometrika, 1972, 37, 29-51.
Brink, N. E., Rasch's logistic model vs the Guttman model, Educational and Psychological Measurement, 1972, 32, 921-7.
Choppin, B. H., The use of latent trait models in the measurement of cognitive abilities and skills. Paper presented at an invitational seminar on 'The Improvement of Testing in Education and Psychology', Australian Council for Educational Research, Melbourne, 1980.
Cliff, N., A theory of consistency of ordering generalizable to tailored testing. Psychometrika, 1977, 42, 375-99.
Cronbach, L. J., Coefficient alpha and the internal structure of tests. Psychometrika, 1951, 16, 297-334.
Cudeck, R., A comparative study of indices for internal consistency, Journal of Educational Measurement, 1980, 17, 117-35.
Gustafsson, J-E., The Rasch model for dichotomous items: Theory, applications and a computer program. Reports from the Institute of Education, University of Gotesborg, No. 63, ED. 154018, 1977.
Gustafsson, J-E., Testing and obtaining fit of data to the Rasch model, British Journal of Mathematical and Statistical Psychology, 1980, 33, 205-33.
Guttman, L., On Festinger's evaluation of scale analysis, Psychological Bulletin, 1947, 44,451-65.
Guttman, L., The basis for scalogram analysis. In S. A. Stouffer (ed.), Measurement and Prediction, New York, Wiley, 1950.
Kuder, G. F. & M. W. Richardson, The theory of the estimation of test reliability. Psychometrika, 1937, 2, 151-60.
Lumsden, J., A factorial approach to unidimensionality. Australian Journal of Psychology, 1957, 9, 105-11.
Lumsden, J., Tests are perfectly reliable. British Journal of Mathematical and Statistical Psychology, 1978, 31, 19-26.
Rasch, G., Probabilistic models for some intelligence and attainment tests, Copenhagen, Danish Institute for Educational Research, 1960. Reprinted by University of Chicago Press, 1980.
Spada, H. & W. F. Kempf (eds), Structural models of thinking and learning, Hans Huber, Vienna, 1977.
Terwilliger, J. S. & K. Lele, Some relationships among internal consistency, reproducibility, and homogeneity. Journal of Educational Measurement, 1979, 16, 101-8.
Wright, B. D. & N. Panchapakesan, A procedure for sample-free item analysis. Educational and Psychological Measurement, 1969, 29, 23-48.
Wright, B. D. & G. A. Douglas, Conditional (CMLE) versus unconditional (JMLE) procedures for sample-free item analysis. Educational and Psychological Measurement, 1977, 37, 573-86.
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/erp7.htm