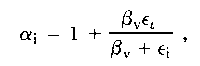
Richard C. Bell
The University of Western Australia
(Research Unit in University Education)
INTRODUCTION
Interest in mental test theories has generally focussed on items rather than persons. This is true of both traditional classical test theory (CTT) which is centered on the item (or test) based notion of reliability and latent trait theories which focus on the item response curve. Concern for what people do in tests has generally been limited to estimating their abilities.
Recently there have been signs of some attempts to consider the person facet of the testing situation in more detail. Lumsden (1977, 1978) has contemplated the potential of using a person response curve and Wright and Stone (1979) have considered the possible patterns of residuals after fitting a Rasch's simple logistic model (SLM) to dichotomously scored test data. Both of these approaches are embedded in the latent trait traditions although it should be noted that the possibility of focussing on person behavior (in contrast to item behavior) was first espoused in a traditional test theory framework by Mosier (1940, 1941).
Clearly, in the approach which formalizes the slope of the person response curve, it is assumed that slopes vary in a meaningful fashion. By contrast, in the approach based on studying residuals from the SLM, it is assumed that any variation among slopes is simply one of a number of forms of misfit. These distinctions parallel those found where items rather than persons are the focus of analysis. Thus when the item discrimination parameter is formalized in a model, it is assumed that variation in the slopes of the item response curves are meaningful. In the SLM, where no discrimination parameter enters the model, simple variation in slope is taken as a particular form of misfit.
The purpose of this paper is to consider the empirical relationship between measures of person fit in the SLM model and measures of the slope of the person response curve which Lumsden (1977) has shown may be interpreted as an index of person reliability.
ITEM FIT AND ITEM DISCRIMINATION
We begin by considering the general situation of a response by person v to item i, and review briefly some item response theory. The probability Pvi as an outcome can be described as a function f(λvi) in which:
| λvi = βv + δi + βv δi + φvi | (1) |
where βv is the person location (ability)
parameter,
δi is the item (easiness) parameter,
βv δi is the interaction term,
φvi is the error,
and where λvi is in a suitable metric such as the
logistic.
The SLM is restricted to the `main effects', βv and δi, and by assuming that βv δi equals zero. If the `interaction' term βv δi is not equal to zero in the data, then the error term
| φ*vi = βv δi + φvi | (2) |
In the Birnbaum (1968) model, an attempt is made to take account of the interaction term βv δi. This is done effectively by a reparameterization which creates an item discrimination parameter αi such that
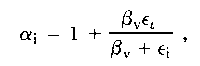
| (1) |
| λvi = αi (βv + εi) + φvi | (4) |
One result of applying (3) is the complication that, for the purpose of parameter estimation, assumptions are required about the distribution of β. No such assumptions are required with the SLM.
The difference between the two models, therefore, can be seen to reside essentially in the interaction term βvεi. In the SLM model, any interaction becomes part of the residual or error term. In model (4), this interaction corresponds to the discrimination term. Thus is would be expected that if data were generated so as to include variation corresponding to the interaction term, but with little random error φvi, there would be a close correspondence between indices indicating the degree of fit to the SLM, and indices corresponding to this interaction term, that is, the discrimination term, in other models.
This relationship has been shown by Bollinger and Hornke (1978). Generating responses of 1,000 persons (with normally distributed ability) to 40 items with varying levels of discrimination, they found an almost perfect curvilinear relationship between the Rasch chi-square index of fit and the discrimination index. Similarly, it could be expected that no discrimination would not affect the fit of the Rasch model and this was also found by Bollinger and Hornke and also by Wood (1978).
PERSON-FIT
By analogy to the term 'item-fit' in relation to items, the term 'person-fit' is used to indicate the degree to which a person's response pattern conforms to the model. The approach to person-fit used here has been discussed fully by Wright and Stone (1979). Their approach was to identify people with abnormal response patterns by evaluating the standardized squares of residuals between the observed response and the `recovered' response according to the model, after taking account of the person and item parameters estimated from the SLM. Various syndromes of misfit were postulated by Wright and Stone. These included `sleeping' or `fumbling' where a person of high ability gets easy items wrong' `guessing' where a person of low ability gets hard items right, and `plodding' where the person behaves `too well', getting all the easy items right and all the hard ones wrong. In the SLM, the standardized square residual simplifies to
| Z²vi = exp[(2xvi - 1)(di - bi)], | (5) |
xvi is the response (0 or 1) of person v to item
i,
di is the estimate of the item difficulty parameter
and
bv is the estimate of the person ability parameter.
Statistical tests of this residual are not straightforward and different approaches have been adopted to produce statistics which may be tested against standard distributions. The approach adopted in the present study was that of Andrich and Sheridan (1980). The statistic they employed was
| t = loge(T) / sqrt( Var(T) ) |
where T = Z²v / fv,
Z² being the standardized square residual for person v summed over all items, and fv being the expected value of this squared residual, alternatively interpreted as the degrees of freedom associated with Z²v.
The statistic t is symmetric with an expected value of 0 and variance of 1. Andrich and Sheridan, who provide a rationale for this statistic, indicated that the distribution should be close to normal and `on the basis of a limited number of simulations . . . seems to work very well' (Andrich and Sheridan, 1980: 18-19).
PERSON RELIABILITY
This concept was introduced by Lumsden (1977, 1978) although the idea had appeared at various times through the previous fifty years in various guises. A trace line identified the probability of a correct response by a person to items scaled by difficulty. If this trace line is assumed to have an ogive (or similar) shape, then the slope of this curve corresponds to person reliability. Such a conceptualization is equivalent to using two parameters for an item response curve, where the slope parameter is equivalent to the item discrimination index of traditional test theory. Consequently, the general model of equation (1) can be considered differently, with the interaction term being parameterized as a function of the person rather than the item, and therefore assuming that the variation within items is zero (Lumsden, 1980).
Unlike the corresponding item response situation, few attempts have been made to define a person based index for this interaction term. Trabin and Weiss (1970), in their study of the Person Response Curve, did not attempt to define reliability parameter for each person, instead they used a residual based approach (as in the Rasch method) from item characteristic curves. Voyce and Jackson (1977), in studying person responses in personality data, used a similar concept which they termed a `subject operating characteristic curve'. They considered two parameters, threshold (ability) and sensitivity (reliability) and estimated these in various ways. A factor analysis of the various estimates (ascending estimate, descending estimate, threshold, biserial, proportion responses, and linear intercept and slope) led Voyce and Jackson to adopt the linear intercept as a threshold measure and the slope as a sensitivity measure.
The biserial measure mentioned by Voyce and Jackson was in fact equivalent to the slope and had been studied previously. Donlon and Fischer (1968) developed this index, terming it the `personal biserial', by correlating person's performance over a set of items with the group performance. This was analogous to the item biserial. Consequently, it may be transformed in the same way to provide person response curve slope parameters. As Lord and Novick (1968) show, for item j
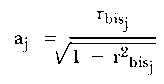
| (7) |
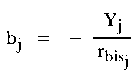
| (8) |
where Yj is the ordinate corresponding to the proportion of correct answers, rbisj. is the item biserial, and aj is the estimate of the item discrimination parameter.
This transformation may also be applied to the Donlon and Fischer index of personal biserial to give Person Response Curve parameters of location and slope.
EMPIRICAL COMPARISON OF PERSON FIT AND PERSON RELIABILITY
(a) Test Items
The test items considered here were 40 verbal items from the Australian Scholastic Aptitude Test (Series F) for 1977. These items could be considered to form a reasonably unidimensional set of items (Bell, 1978). All items were of the reading comprehension type, i.e. `nested' under a series of passages.
(b) Subjects
The subjects were 350 twelfth grade males studying predominantly humanities/arts-based subjects in their final year of secondary schooling and were a random sample of the 1366 such students in Western Australia in 1977.
(c) Person Measures (Location and fit/reliability)
(i) The Rasch error and fit measures were as described in Section 3 above.
(ii) The Person Response Curve measures included the raw score and a number of Person Response Curve possibilities. These included the simple point biserial correlation between item response and item difficulty, the transformation of this to a logistic biserial (following Jensema, 1976), and a second transformation via the logistic distribution to slope and location parameters as in (5) and (6). In addition to this, two other variants were considered. One was to use a simple logistic transformation on the proportion right to set the location parameter. This was considered because the estimation of location depends on slope and thus when the slope is near zero (i.e. rpbis -> 0) location can become extreme as evident in (6) above. The other variant was to use a prior monotonic transformation on the responses to `smooth' the data using isotonic regression of item response on logistic scaled item difficulty following Ramsay (1972) and others. To accommodate estimation from these isotonic regressed responses, the calculation of the point biserial followed normal product moment procedures rather than the differences between means approach usually associated with the point biserial.
An example of a person's responses and fit is shown in Figure 1.
|
FIGURE 1 Example Person Response Curve (PRC) |
|---|
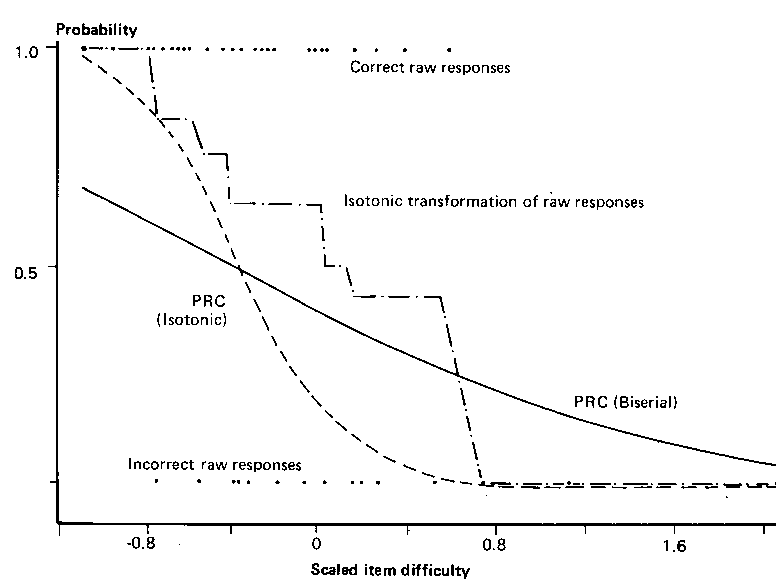
|
Unfortunately, there was a preponderance of easy items as shown by the raw responses on the low end of the scale, both correct and incorrect. The isotonic transformation regularized the tendency for right and wrong items to be mixed. In Wright and Stone's terminology, this means that the response patterns were modified from reflecting "fumbling" to reflecting "plodding".
The smooth Personal Response Curve derived from the isotonic regression (the dashed line) was, as a consequence, much steeper in slope than that of the curve derived through the raw biserial transformation (the solid line).
(d) Methods and Results
The various parameters were correlated. Thirty-one persons were deleted from the analyses because of the outlying values obtained. Principally, these were due to values of location for the curves which were greater than 5.0 (absolute), these being obtained for slope values near zero (as could be expected from the formulae in section 4). Some (eight) were eliminated because of extreme errors of fit in the Rasch analysis.
Means and standard deviations are shown for the parameters in Table I and correlations in Table II.
|
TABLE I Means and Standard Deviations for Person Response Curve Parameters and Rasch Person Fit Statistics | ||
|---|---|---|
| Variable | Mean | Standard Deviation |
| Raw Score Point Biserial Person Biserial PRC Location PRC Slope Isotonic R Isotonic Location Isotonic Slope Loge ability Rasch ability Rasch measurement error Rasch fit | 21.21 .29 .37 .05 .43 .85 .07 1.75 .26 .13 .35 .09 | 5.86 .14 .19 1.38 .26 .07 .45 .47 .20 .70 .02 .88 |
| Based on 319 persons. | ||
|
TABLE II Correlations among PRC Parameters and Rasch Person Parameters for Verbal Subscale and Male Arts Sample (Decimals Omitted) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Raw Score Point Biserial Person Biserial PRC Location PRC Slope Isotonic R Isotonic Location Isotonic Slope Loge ability Rasch ability Rasch measurement error Rasch fit | - 32 37 78 38 37 97 42 99 99 38 -17 | - 99 25 94 46 31 42 31 32 -06 -91 | - 28 97 43 38 39 37 39 -00 -90 | - 26 38 74 40 78 76 30 -12 | - 42 37 37 37 39 03 -84 | - 30 91 37 31 -06 -42 | - 34 96 99 35 -17 | - 42 37 06 -36 | - 98 32 -15 | - 40 -18 | - -03 |
Product moment correlations did not always accurately describe the relationship between the parameters, as there were curvilinear relationships between some parameters. Figure 2 shows the relationship between the slope of the Person Response Curve and the fit statistics for the SLM to be slightly curved, but one which could be explained largely by a linear trend, the correlation being - 0.84. As can be seen from Table II the biserial indices in fact gave even greater correlations.
FIGURE 2
|
FIGURE 2 Scatterplot of Person Response Curve Slope and Rasch Fit Index |
|---|
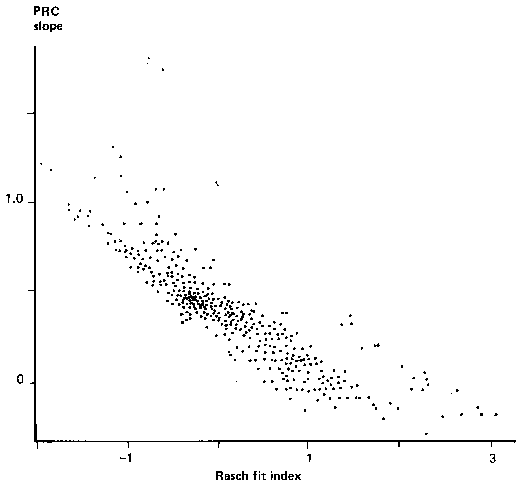
|
To simplify the relationships in Table II a principal components analysis with varimax rotation was carried out on the correlations. The Kaiser-Guttman rule gave three components which accounted for 90% of the variance. The results are shown in Table III.
|
TABLE III Varimax Rotated Principal Component Loadings of Correlations among PRC Parameters (Major Loadings Only, Decimals Omitted) | ||||
|---|---|---|---|---|
| Parameter | 1 | Factor 2 | 3 | Commmunality |
| Raw Score Point Biserial Person Biserial PRC Location PRC Slope Isotonic R Isotonic Location Isotonic Slope Loge ability Rasch ability Rasch measurement error Rasch fit |
95 81 94 94 96 |
97 97 95 -95 |
81 76 |
98 98 99 70 96 90 96 84 95 98 56 93 |
The three factors clearly revealed the relationships among the parameters. The first factor was the PRC location parameter, where the direct estimation of the PRC location parameter was seen as less related to this factor than the other measures. The second factor was the PRC slope parameter and it was seen that the SLM fit index was very similar to the correlation/PRC slope indices. The third factor isolated the monotone transformed correlation and slope.
DISCUSSION AND CONCLUSIONS
This research note has shown that for real data a relationship can be seen between measures of person reliability and an index of person fit in the SLM. This fit is not as perfect as the results of Bollinger and Hornke (1978) indicated for items with Monte Carlo data. However, it was substantial enough to indicate that the various possible patterns of residuals suggested by Wright and Stone (1970) in fitting the Rasch model, were dominated by a component corresponding to the slope of the Person Response Curve. This could be partly a function of the data where the multiple choice format could lead to effects of guessing on the lower asymptote; and partly due to the fact that possible patterns of misfit are accommodated by effects on the slope of the PRC.
These results were supported by a principal component analysis of a number of possible indices for this curve, which showed a two parameter structure for these indices as was found by Voyce and Jackson (1972) for personality data.
This research note has highlighted a distinction between Rasch and other models. The distinction is not one of correctness or validity, but rather one of appropriateness. More studies are required to give us some idea of the extent to which this systematic slope component can be found in various forms of real test data. It may be conceivable that different models are appropriate for different kinds of data. Another kind of appropriateness is one of purpose. Because of its optimal statistical properties the Rasch model is the most effective prescriptive model but the fewer parameters used means that it is less effective as a descriptive model. It would thus seem important to consider the purposes of an analysis in choosing a model, that is, whether future use of the test requires robust data, or whether a full description of a single test situation is required. For some data this choice may not be needed in the future. Andrich (1982) has shown that for data other than binary, the Rasch model may be extended to parameters of discrimination following a parallel conceptualization of Guttman's components of scaling.
Person Fit and Person Reliability, Richard C. Bell
Education Research and Perspectives, 9:1, 1982, 105-113.
REFERENCES
Andrich, D., An extension of the Rasch model for ratings providing both location and dispersion parameters. Psychometrika, 1982, in press.
Andrich, D. & B. E. Sheridan, RATE: A fortran IV program for analyzing rated data according to a Rasch model. Research Report No. 5. Department of Education, University of Western Australia, 1980.
Bell, R. C., The structure of ASAT-F: A radial parcel double factor solution. In Research Papers relating to the Australian Scholastic Aptitude Test. Hawthorn, Vict.: Australian Council for Educational Research, 1978.
Birnbaum, A., Some latent trait models and their use in inferring an examinee's ability. In F. M. Lord and M. P. Novick. Statistical theories of mental test scores. Reading, Massachusetts, Addison Wesley, 1968.
Bollinger, G. & L. F. Hornke., On the relation of item discrimination and Rasch scalability. [Uber die Bezierhung von Intemtrennscharfe and Rasch-Skalierbarkeit.] Archiv fur Psychologie, 1978, 130, 89-96.
Donlon, T. F. & F. E. Fischer, An index of an individual's agreement with group-determined item difficulties. Educational and Psychological Measurement, 1968, 28, 105-13.
Jensema, C., A simple technique for estimating latent trait mental test parameters. Educational and Psychological Measurement, 1976, 36, 705-15.
Lord, F. M. & M. R. Novick, Statistical theories of mental test scores. Reading, Mass.: Addison Wesley, 1968.
Lumsden, J., Person reliability. Applied Psychological Measurement, 1977, 1, 477-82.
Lumsden, J., Tests are perfectly reliable. British Journal of Mathematical and Statistical Psychology, 1978, 31, 19-36.
Lumsden, J., Variations of a theme by Thurstone. Applied Psychological Measurement, 1980, 4, 1-7.
Mosier, C. I., Psychophysics and mental test theory. Fundamental postulates and elementary theorems. Psychological Review, 1940, 47, 355-66.
Mosier, C. I., Psychophysics and mental test theory. II The constant process. Psychological Review, 1941, 48, 235-49.
Ramsay, F. L., A Bayesian approach to bioassay. Biometrics, 1972, 28, 841-58.
Trabin, T. E. & D. J. Weiss, The person response curve: Fit of-individuals to item characteristic curve models. Minneapolis: University of Minnesota, Department of Psychology, Psychometric methods program, December, 1979.
Voyce, C. D. & D. N. Jackson, An evaluation of threshold theory for personality assessment. Educational and Psychological Measurement, 1977,37, 383-408.
Wood, R., Fitting the Rasch model - a heady tale. British Journal of Mathematical and Statistical Psychology, 1978, 31, 27-32.
Wright, B. D. & M. Stone, Best test design. MESA Press, Chicago, 1979.
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/erp8.htm