Category Characteristic Curves for
Positively and Negatively Worded Statements
Combined.
Research Note
Leonie J. Rennie
The University of Western Australia
The measurement of non-cognitive variables is subject to response bias, or response set. This is the tendency of a person to respond to questions in a particular way independently of the content of the questions or, as conventionally termed, items. There are many kinds of response biases: for example, the tendency to agree rather than disagree, or the tendency to make extreme responses. Twenty years ago, Messick (1962) wrote:
On the one hand these response sets are confounded with legitimate replies to item content and hence introduce errors of interpretation into the logical validity of scales, but on the other hand response styles are also stable and reliable components of performance, which may reflect consistent individual styles or personality traits. (Messick, 1962: 41)
Kerlinger (1973: 497) believes that `while response set is a mild threat to valid measurement, its importance has been overrated'. More recently, Lehmann (1980) indicated that more research was needed on response sets, including the kinds of people susceptible to response set; on the kinds of items and tests affected by response sets; and on whether or not their effect could or should be neutralized.
While the effects and importance of response set or bias remain equivocal, it is important that a test constructor becomes aware of items which, because of some peculiarity or other, elicit a response bias. The purpose of this research note is to draw attention to a response bias evidenced in some items of a Likert-type attitude scale, and to the way this response bias was detected.
Affective scales are usually developed so that approximately half of the items are worded in the positive direction (so that agreement to such items represents a positive attitude), and the remaining items are worded in the negative direction (so that disagreement to such items represents a positive attitude). Further, the items are usually presented in a random order.
The reason usually given for these procedures is to decrease the possible effects of an agreement or a disagreement response bias. A person with an agreement response bias, for example, who tends to agree rather than disagree with each item, would achieve a score which is an overestimate of his or her attitude if all items are worded in the positive direction, or an underestimate if all the items are worded in the negative direction. With equal numbers of positively and negatively worded items, it is intended that the summed score is a more accurate representation of the person's attitude, with the effects of the response bias cancelled out. This hope will be forlorn, however, if some property of the wording or content of particular items tends to elicit response bias.
Just such a property has been found in a Likert-type instrument constructed to measure students' interest in school science. In a Science Rating Scale (Rennie, 1980), students were asked to respond either Strongly Disagree, Disagree, Agree or Strongly Agree to each of twelve items, and these responses were scored 0, 1, 2 or 3 respectively for the six items which were worded positively, and 3, 2, 1 or 0 for the remaining six items which were worded negatively. Test data for 357 respondents were analyzed according to the Rasch Rating Model (Andrich, 1978) using the computer program RATE (Andrich and Sheridan, 1980), and some of the results are reported elsewhere (Rennie, 1980).
In general terms, the data accorded well with the rating model. The mean person attitude value was found to be 0.21, indicating that, on average, and compared with the imposed origin of 0.0 to the items, students tend to have a positive attitude toward their school science. Estimates of item affective values were compared with item wording and the ordering of items was found to be reasonable on intuitive grounds. The person separation index value [= Rasch reliability], analogous to Cronbach's α in meaning and similar in value, was 0.87, implying a high power for the various tests of person-fit and item-fit.
An inspection of item-fit and person-fit statistics indicated that the response patterns of three items (Item 1 which was negatively worded, and Items 5 and 10, both of which were positively worded) and of 14 persons, showed signs of misfit and should be given closer investigation. Inspection of the 14 person response patterns (see Rennie, 1980) revealed that the discrepancies between observed and expected scores were spread over the items rather than being concentrated on several particular items. Even though Items 1, 5 and 10 gave indications of misfit, these items were not particularly prominent in the response patterns of persons who showed misfit.
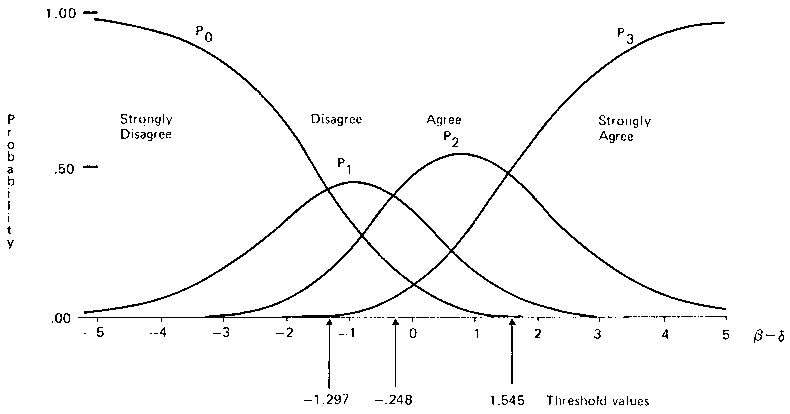
The issue in this paper, however, is not concerned with the statistical tests of fit associated with items or persons, but with a different kind of fit. It is concerned with an observation which violated an intuitive expectation regarding a symmetrical relationship in the estimates of the thresholds on the rating continuum. Thus it was expected that the two distances between the three successive thresholds would be approximately equal. Instead, the estimates of the successive thresholds were - 1.30, - .25 and 1.56 where clearly, distances between the ordered successive thresholds were not equal. The distance of 1.81 between the second and third thresholds is nearly twice the distance of 1.05 between the first and second thresholds. This difference reflects an over use of the `Agree' category compared with the `Disagree' category.
These estimated values are translated into a set of probabilities of response curves in Figure 1. In Figure I, the horizontal axis represents the difference β - δ between a person's attitude, parameterized by β, and the item's affective value, parameterized by δ. According to the Rating Model (Andrich, 1978), the probability of responding `Strongly Disagree' is greatest when β - δ is large and negative, that is, when the person has a low attitude value and the item has a high affective value. Conversely, when the person has a high attitude value and the item has a low affective value, β - δ is large and positive, and the probability of responding `Strongly Agree' is greatest.
The graph in Figure 1 shows that this is so for the Science Rating Scale.
| FIGURE 1 Category Characteristic Curves for Positively and Negatively Worded Statements Combined. |
|---|

|
However, when the scale position of a person and item is identical (and β - δ = 0) it might be expected that the probability of a person responding 'Disagree' or 'Agree' would be the same. Figure 1 shows that this is not the case when β - δ = 0 the most probable response is `Agree'. It is clear that the `Disagree' category will be used less often. (For negatively worded items, it is the `Agree' category which is underused.)
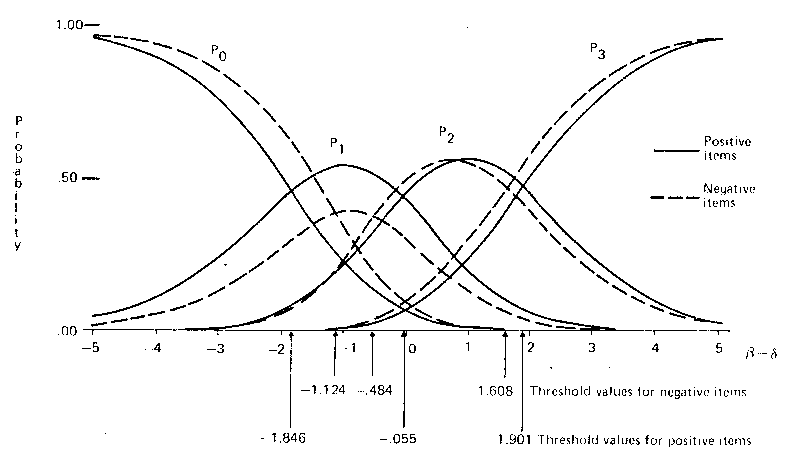
In seeking a further understanding of the asymmetry in threshold values, a first step chosen was to consider the items in sub-sets, where an obvious division is to separate the positively and the negatively worded items. Each of these sets was analyzed separately according to the same rating model as the total set.
For the positive items, the new estimates for the threshold parameters were -1.85, -.06 and 1.90. With successive differences of 1.79 and 1.96, greater symmetry in response patterns is evidenced than with the total set of items. In contrast, for the negative items, the estimated threshold parameters were -1.12, -.48 and 1.61, where the distance of 2.09 between the last two thresholds is more than three times greater than the distance of 0.64 between the first two.
| FIGURE 2 Category Characteristic Curves for Positively and Negatively Worded Statements Separated. |
|---|
|
The differences in symmetry in response sets between the two subsets of items are emphasized in Figure 2. The main difference is related to the lower probability of scoring 1 on the negatively worded items (that is, a lower probability of responding `Agree' to the item content) and the corresponding higher probability of scoring 0 (that is, responding `Strongly Agree'). A second difference is that when β - &detla; is positive, there is a greater tendency to score 3 rather than 2 on the negatively worded items, compared with the positively worded items. The total probability of scoring 2 on an item is similar for both kinds of items. From Figure 2, it can be inferred that when an item is worded negatively, rather than positively, there is a greater tendency to respond in the extreme categories, and in particular, a greater tendency to strongly agree, rather than agree. This suggests a response bias to negative items, but not to positive items.
This conjecture is based on a particular grouping of items, and offers no proof that the direction of wording is the sole reason for the difference in symmetry in the threshold parameters. If this were so, the wisdom of combining the items into a single measure would be questioned. One way to clarify this issue is to examine the category characteristic curves for individual items. An examination of these showed that although the positively worded items were behaving similarly, with equal use of the agree and disagree categories, the negative items were not. Item 8, for example, had a response pattern similar to the positively worded items, while the item characteristic curves for Items 2 and 4 showed marked underuse of the `Agree' category (scored 1) and marked overuse of the `Disagree' and `Strongly Agree' categories (scored 2 and 0, respectively).
It might be concluded from these observations that the differences in the response curves shown in Figure 2 are not wholly dependent upon the direction of wording in the items, but dependent also upon item content. Items 2 and 4 have very similar meaning -`I find it hard to get down to work in science classes' and `My mind wanders off the subject during science lessons' - it is possible that a student's ability to concentrate is interacting with his interest in science. While a factor analysis of the Science Rating Scale, which was also carried out on the data, supported the proposition that Items 2 and 4 were measuring a separate dimension, the results of a factor analysis did not reveal the cause of such inconsistent response patterns. It is interesting to note that only Item 2 showed possible misfit on one of the tests of item-fit when analyzed using Rasch methodology. Further, traditional item statistics suggested a homogeneous scale, Cronbach's α had a value of 0.90, and item-part correlations ranged between .49 and .77. (Items 2 and 4 had item-part correlations of .56 and .59, respectively.) The similarity of these two items, and the likelihood that they are measuring another dimension with a very specific manifestation may have been missed easily if their category characteristic curves had not been examined. In turn, these curves may not have been given close attention if the question of response bias had not been investigated on the basis of the asymmetrical threshold values in the first analysis.
Research Note: Detecting a Response Set to Likert-style Attitude Items with the Rating Model, Leonie J. Rennie
Education Research and Perspectives, 9:1, 1982, 114-118.
REFERENCES
Andrich, D., A rating formulation for ordered response categories. Psychometrika, 43, 1978, 561-73.
Andrich, D. & B. E. Sheridan, RATE: a fortran IV program for analyzing rated data according to a Rasch model. Research Report No. 5, Department of Education, University of Western Australia, 1980.
Kerlinger, F. N., Foundations of behavioral research (2nd ed.). London: Holt Rinehart & Winston, 1973.
Lehmann, I. J., Measuring affect. Australian Educational Researcher, 7, 3, 1980, 29-52.
Messick, S., Response style and content measures from personality inventories, Educational and Psychological Measurement, 22, 1962, 41-56.
Rennie, L. J., Rasch models and person fit analyses: interpreting unlikely response patterns. Research Report No. 9, Department of Education, The University of Western Australia, 1980.
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/erp9.htm