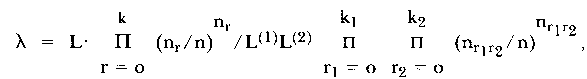
An unconditional likelihood ratio test is suggested, to test the assumption of item homogeneity in the Rasch model. The test statistic is asymptotically chi-square distributed for increasing numbers of items and persons. Simulation studies show the practicability of this goodness of fit test even for smaller item numbers. The sensitivity towards various types and different degrees of violation of the item homogeneity assumption has also been investigated by means of simulated data.
Introduction
The question whether or not the logistic model of Rasch (1960) holds true for a set of data cannot be answered on the basis of a single statistical test. There are two reasons for this. Firstly, there is no set of axioms for the Rasch model which can be tested directly for violations by means of the empirical data for which the model is developed (i.e., only one reaction of each person to each item). Secondly, in each test of significance for the model its adequacy for a given set of data is formulated in the null hypothesis. One can never verify the model (under a certain probability), but only fail to falsify it. Thus as many different assumptions of the model as possible should be tested empirically in order to make the assertion that the model fits the data.
Gustafsson (1980) discusses this point in terms of the assumptions of unidimensionality, local statistical independence and homogeneity of item discrimination. He concludes,
that the Rasch model assumptions can be violated in basically two ways: either a model is needed to describe the data which contains two or more parameters for each person, which would be a violation of the assumption of unidimensionality; or a model is needed which contains two or more parameters for each item, which would be a violation of the assumption of the form of the item characteristic curves; or, of course, a combination of these (209).
This conclusion can also be described in variance-analytic terminology: the basic assumption of the Rasch model (1) is the negation of an interaction between person ability βv and item easiness σi with respect to the solution probability p(xvi).
| p(xvi) = exp(xvi(βv + σi))/(1 + exp(βv + σi)) | (1) |
where xvi = 1, when person v solves item i, 0, otherwise
βv ... person parameter
σi ... item parameter.
(See paper by R. Bell this issue.)
This basic assumption is specific for the Rasch model and is not made, for instance, in the model of Birnbaum (1968) or the latent class model (Lazarsfeld and Henry 1968). In the latter, varying item parameters can be valid for different persons, namely, when they belong to different latent classes (cf. (2)).
| P(xvi) = πgixvi - (1 - xvi) πgi | (2) |
where πgi is the item parameter for all persons who belong to the latent class g(0 < πgi < 1)
This assumption of no interaction can be expressed in a somewhat more differentiated manner using the two concepts of person homogeneity and item homogeneity. Person homogeneity refers to the characteristic of a test model to assume that all persons work on the items of a test on the basis of the same latent ability. Thus any differences between persons is expressed in a variation in their ability parameters and not in different item parameters for different persons.
Analogously, item homogeneity means that all items affect the same latent ability in each individual person. Differences among items may only be expressed in different difficulty parameters. It is not possible for one and the same person to answer different items with different degrees of ability. To accentuate the apparent paradox in these definitions, personal heterogeneity is reflected in different item parameters for different groups of persons; item heterogeneity is expressed in varying person parameters for different item groups.
Does it make sense to discriminate between these two concepts - item homogeneity and person homogeneity when both only lend expression to the basic assumption that there is no interaction between person ability and item difficulty?
The example of the latent class analysis shows that it at least might be meaningful; this model presupposes item homogeneity, but not person homogeneity. The Rasch model, on the other hand, postulates both kinds of homogeneity. To test the fit of the Rasch model, therefore, means both: to test person homogeneity and item homogeneity. The former is done by checking if more than one item parameter for each item is needed to describe the data, the latter by checking if more than one person parameter for each person is needed. It is obvious that the conditional likelihood ratio test presented by Andersen (1973a) primarily tests person homogeneity in this terminology. Only under certain conditions is the Andersen-test sensitive to violations of the assumption of item homogeneity (cf. Gustafsson 1980).
For the purpose of testing item homogeneity directly, an analogous test is needed, which renders it possible to test whether all items are solved on the basis of one parameter for each person. A straightforward way of doing this is to divide the item-population into two or more subgroups, to estimate the person parameters for each of these item groups separately, and to decide by means of a statistical test whether or not they are different from each other. This article deals with such an approach. A technical aspect of the data analysis has some disadvantages due to the fact that the unconditional maximum likelihood method (JMLE) is used. An analogous test using the conditional maximum likelihood method has been developed by Martin-Löf (1973) and is discussed in Gustafsson (1980) in some detail. Although the conditional approach has advantages in the case of a small number of items, the unconditional approach has similar properties with large numbers of items and is, in this case, easier to compute since no elementary symmetric functions of the item parameters have to be computed.
The unconditional likelihood ratio
The hypothesis to be tested is, whether the person parameters of the Rasch model are invariant, up to the addition of a constant term, for the m disjoint subgroups of items in a given test. The statistical null hypothesis is therefore:
| H0 = βv1 = βv2 + d2 = ... = +βvj + dj = βvm + dm | (3) |
for all persons v and all subtests j (j = 1,..., m). For the simpler manner of writing of the Rasch model (I') with multiplicative parameters θv = exp(βv) and εi = exp(σi), customarily used for the derivation of estimation equations,
| p(xvi) = (θvεi)xvi/(1 + θvεi) | (1') |
the null hypothesis is:
| H0 = θv1 = c2θv2 = ... = cjθvj = cmθvm | (3') |
The basic consideration for the likelihood ratio test (LR test) is the following: if the person parameters for the various item groups do not differ at all (or only by a multiplicative or additive constant), the likelihood of the entire data matrix L under the assumption of one parameter per person is only slightly smaller than the product of the likelihoods L(j) (j = 1, . . ., m) of the sub-matrices which encompass only the items of group j.
It must be possible to test the assumption of homogeneous item subgroups by testing the likelihood ratio (4) for deviation from 1.
| λ = L/ Πj=1m L(j) | (4) |
The question arises, whether or not it would be possible to use the conditional likelihood functions for the computation of this likelihood ratio. The advantage of such a conditional approach would be that the estimates of the incidental parameters, i.e., the person parameters, are not part of the likelihood functions; hence the value of λ is not affected by the accuracy of the estimation of these parameters. On the other hand, the statistical null hypothesis (3 resp. 3') refers to the person parameters and it is difficult to imagine that this hypothesis could be tested without estimating the person parameters for the different subgroups of items.
Martin-Löf (1973) has shown, that it is possible to construct such a test statistic, which is based on the maxima of the conditional likelihood functions. He proved that -2 ln λ is asymptotically χ2-distributed, when the likelihood ratio (4) consists of the conditional functions multiplied by simple factors depending on the sufficient statistics for the ability parameters. For the case of only two item groups this conditional likelihood ratio is
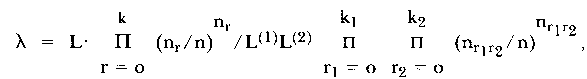 |
(5) |
where k denotes the total number of items, k1 and k2 the numbers in each subgroup so that k = k1 + k2. Furthermore n is the total number of persons, nr the number of persons with a raw score r in the entire test and nr1r2 the number of persons with raw score r1 in the first set of items and score r2 in the second set. L is the maximum of the following likelihood function
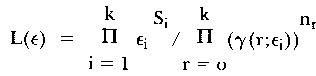 |
(6) |
of the item parameters εi, when Si is the number of persons who solved item i and γ(r;ε) is the elementary symmetric function of order r in the parameters ε. The likelihoods L(1) and L(2) are analogously defined. The asymptotic χ2-distribution of - 2 In λ for n -> infinity has k1k2 - 1 degrees of freedom. For a more detailed discussion of this test see Gustafsson (1980).
In the following, the unconditional approach to the same problem of testing item homogeneity is discussed. As the literature of the Rasch model shows, both approaches - the conditional and the unconditional - have their own advantages - customarily the former one from a more theoretical point of view and the latter one under some practical considerations, such as computer time. This is also true for the Martin-Löf test and the following one.
A test statistic is suggested in which the likelihood ratio (4) is computed on the basis of the unconditional likelihood functions
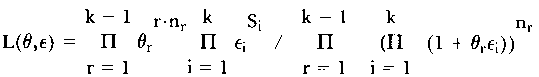 |
(7) |
of the person parameters θ and the item parameters ε. While L in (4) stands for the maximum of this function, when each person has only one ability parameter &thetav for solving all items, L(j) denotes the analogous likelihood for item groups j under the assumption of special person parameter estimates (θ(j)) for each of these groups. It becomes clear that-when the null hypothesis (3) is valid -λ differs only insignificantly from 1; the product of the likelihoods L(j) - when parameter estimates θv(j) are identical for all j - is equal to the numerator of λ. The more the abilities of the persons vary across the different item groups, the more λ diverges from 1; the numerator of λ, which is the likelihood of the data under the assumption of one parameter per person, becomes smaller than the denominator.
According to Kendall & Stuart (1973), the test statistic Z = -2 ln λ for such likelihood ratios is asymptotically χ2-distributed when the likelihood functions included in supply consistent, asymptotically normally distributed estimates. The number of degrees of freedom corresponds to the number of parameters to be estimated, by which the null hypothesis (numerator of λ) differs from the alternative hypothesis (denominator of λ). In the case of n tested persons, these are:
| df = (m.n+k-m) - (n+k-1) = (m-1).(n-1) | (8) |
The crucial point in connection with the suggested LR test is that the precondition of consistent estimates for n-> infinity where the item number k is constant, is not satisfied for the unconditional likelihood function (7). As Neyman & Scott (1948) have shown, the characteristics of consistency and efficiency - normally given in ML estimates - are not necessarily given when the probabilistic model contains parameters whose number tends to infinity with increasing number of observations (so called incidental parameters). This is the case in the Rasch model; when one increases the number of observations by testing more persons, the number of parameters contained in the model increases too, namely by one parameter for each additional person.
Andersen (1973b) showed in the case of two items, that the unconditional ML estimates are actually inconsistent. Wright & Douglas (1977) demonstrated this for the general case of an arbitrary number of items by showing the inequality of unconditional and conditional estimators, whereby consistency has been proved for the latter (Andersen 1970). The estimation error has the effect that the variance of the parameters is overestimated, that is, the estimates of easy items are too high and of the difficult ones too low (Fischer 1974). It has been shown in simulation studies that this error can be counterbalanced by the correction factor (k - 1)/k for the logarithmic item parameters (with norming: Σσi = 0) (Fischer & Scheiblechner 1970; Wright & Douglas 1977):
| (9) |
Since this correction factor (k - 1)/k for k-> infinity tends towards 1, that is, the error becomes less when the number of items increases, it could be expected that the unconditional ML estimation equations for n-> infinity and k-> infinity are consistent. This was proved by Haberman (1977).
What is the result of these findings for the unconditional LR test (4)? As Andersen (1971) demonstrates on the basis of examples, the asymptotic chi-square distribution for Z = -2 ln λ is not necessarily valid when the likelihood functions included in λ are inconsistent because of incidental parameters. Due to the consistency of the parameter estimates for k-> infinity it could be expected that the test statistic Z for the unconditional LR is still chi-square distributed when there is a sufficiently large number of items. For a smaller number of items greater divergencies from the chi-square distribution should occur. The primary concern of the simulation study discussed in the following section is to test this and to compare the strength of the distortion with the effects resulting from the failure of the null hypothesis, that is, item heterogeneity.
Results of a Simulation Study
(I am indebted to Holger Sonnichsen for writing the computer program.)
Through the generation of random item responses, on the basis of various model structures and the subsequent calculation of the suggested likelihood ratios for testing item homogeneity, the following questions should be answered:
(i) Does the distribution of the test statistic -2 ln λ for increasing numbers of items approximate the chi-square distribution?
(ii) How great are the divergencies from the chi-square distribution, caused by small numbers of items, in comparison with those divergencies which result from a varying degree of violation of the null hypothesis?
(iii) Is This goodness of fit test sensitive to violations of the assumption of person homogeneity?
(iv) Does a better approximation to the chi-square distribution result from low numbers of items when λ is computed on the basis of the corrected item and person parameters?
In order to answer these questions, data matrices for the following parameter distributions were generated:
Model structure A (Rasch homogeneity):
450 persons divided into 3 subgroups of equal size with different ability parameters θ1, θ2 and θ3, and with responses to k items of which one half has a low easiness parameter (ε1 = 0.5) and the other half a high easiness parameter (ε2 = 2.0) (cf. Fig. 1a).
Model structure B (person heterogeneity):
The distribution of the person parameters corresponds to that of model structure A, however, for 50% of the persons in each group different item parameters are valid for half of the items (cf. Fig. lb).
Model structure C (item heterogeneity):
The distribution of the item parameters corresponds to that of model structure A, however, for 50% of the items different ability parameters are valid for two-thirds of the persons (cf. Fig. I c).
|
FIGURE 1 Three types of model structures used to generate random data matrices. | ||
|---|---|---|
| a. model structure A: RASCH homogeneity |
b. model structure B: person heterogeneity |
c. model structure C: item heterogeneity |
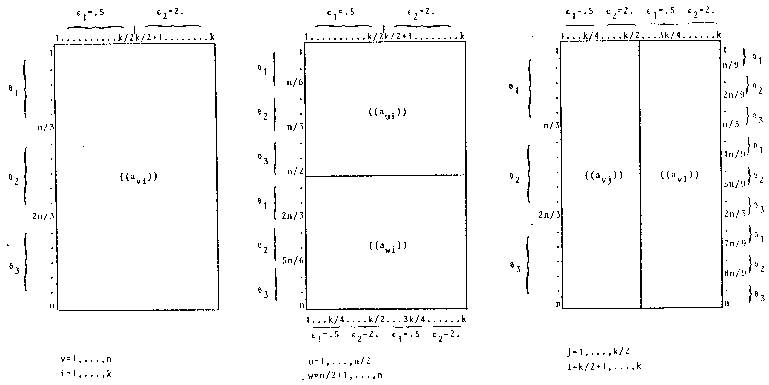 | ||
The following were varied for all three model structures
- numbers of items: k = 8; k = 16; k = 32
- variation in abilities:
θ1 = 0.2, θ2 = 1,
θ3 = 5
θ1 = 0.33, θ2 = 1,
θ3 = 3
θ1 = 0.5, θ2 = 1,
θ3 = 2
θ1 = 0.75, θ2 = 1,
θ3 = 1.33
To compute the likelihood ratio (4) two equally large item groups were formed: in model structures A and B all odd and all even items were combined. In model structure C, where there really are two heterogeneous groups of items, λ was calculated for different item groupings in such a way that the relationship of heterogeneous items in each of the two item groups varied from (k/4) : (k/4) to (k/2) : 0.
These last item groupings in model structure C reflect different `degrees' of violation of the statistical null hypothesis in the sense that the true partition of the items into two heterogeneous groups has been `captured' more or less by means of the hypotheses of the test constructor. Thus, those cases of empirical testing practice are simulated where it is assumed - correctly - that a test encompasses two heterogeneous groups of items but, for a certain number of items, classification is carried out incorrectly.
`Degrees' of violation of the statistical null hypothesis in another sense are simulated in model structure C because the variance of person abilities (for both groups of items) differs: when the variance is small (θ1 = 0.75; θ3 = 1.33) the mean differences between the abilities with which a person solves both groups of items is not large either. Item heterogeneity is then `less' than when person abilities vary greatly (θ1 = 0.2; θ3 = 5), where differing abilities for items of equal difficulty also mean considerably greater differences in the response probabilities
A third variable in which a differing degree of violation of the item homogeneity assumption could be expressed, namely, the correlation of person parameters for the heterogeneous item groups, did not vary: it is always r = 0.0 (cf. Fig. lc). Stated in correlation statistical terminology, we are dealing with independent subtests. With respect to the definition of item heterogeneity provided in the beginning, we are dealing with a mean degree of heterogeneity since the intra-individual ability differences would be greater if there were a negative correlation.
| FIGURE 2 |
|---|
| Mean Z-values for Rasch homogenous (A), person heterogeneous (B) and item heterogeneous (C) data matrices with 8, 16 and 32 items. Four different ranges of ability parameters as well as different modes of item grouping in matrices with model structure C were used to vary the `degree' of item heterogeneity. The common probability levels of the chi-square distribution with 449 degrees of freedom are marked. |
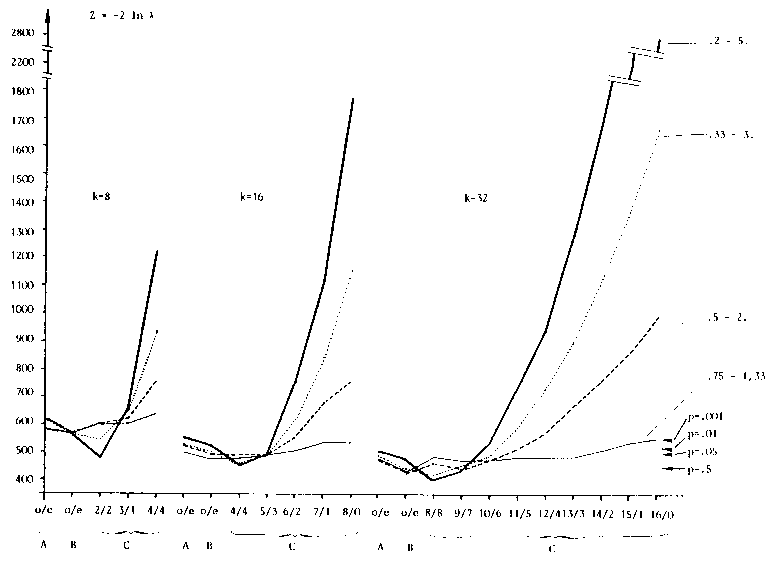 |
The results are depicted in Fig. 2. The mean value of the test statistic Z = - 2 ln λ is plotted there on the ordinate for the different numbers of items, model structures and item groupings. Each of these mean values are based on 10 simulated data matrices. With regard to the four questions of investigation the results can be summarized as follows:
(i) in a Rasch-homogeneous test (model structure A) consisting of 8 items, the Z values are higher than the 1 per cent limit of chi-square distribution with 449 degrees of freedom. For 16 items the values lie between the 5 per cent and 1 per cent level. For 32 items all values are below the 5 per cent level, i.e. are not significant in the customary sense. Thus the question about the asymptotic chi-square distribution of - 2 ln λ for k-> infinity can be answered positively: for 30 or more items work can be done with the `normal' significance boundaries.
(ii) The course of the curves for the item groupings which correspond with the correct grouping to varying extents, in a test consisting of two Rasch-homogeneous subtests (model structure C) is strongly ascending and positively accelerated for increasing correspondence. In the instances where the distribution of heterogeneous items over the two groups of items is no better than a random distribution, that is, 2 heterogeneous items each in both halves of the test with 8 items, 4 each when there are 16 items and 8 each when there are 32 items, the Z values are approximately as high as, sometime lower than, in a Rasch-homogeneous test. This coincides with the expectations since, where such distributions are concerned, `mean' person abilities are estimated for both halves of the test. These person abilities do not diverge systematically from one another. For 3 out of 4, 6 out of 8 and 11 out of 16 correctly classified items the Z values are already significantly above the significance level and also above the mean Z values of Rasch-homogeneous tests. For greater portions of correctly classified items the Z values increase so rapidly that the contention that the LR test is also useful where smaller numbers of items are concerned is justified as long as the tested a priori hypotheses about heterogeneous items are `good' in the sense of correct item groupings. `Useful' then means, however, that one must test extremely conservatively, that is, select an unusually low significance level for small item numbers.
The variance of person parameters has remained uninterpreted as a factor which also influences the degree of item heterogeneity and the size of Z. As expected, the slope of the curves becomes smaller for decreasing variances. Only as far as the smallest of the variances used here, (θ1 = 0.75, θ2 = 1.0 and θ3 = 1.33) is concerned the effects of item heterogeneity on X are too small to be detected reliably by means of this likelihood ratio. But this is a very extreme case of inter- and intra-individual differences: in the exponential version of the Rasch model (1) the range of abilities would be from ξ1 = - .29 to ξ3 = + .29. In all cases of substantial variances of abilities the effects of item heterogeneity are so strong, that the conclusion may be drawn, that the LR test makes sufficiently reliable statistical decisions possible.
(iii) As can be seen from the Z values for model structures B, the test is not sensitive to violations of the assumption of person homogeneity. This is the analogous result to the already mentioned fact that the CLR test of Andersen (1973a) only tests person homogeneity, not item homogeneity. Analogous to this, person heterogeneity leads to significant Z values only under certain conditions, which were not fulfilled in the simulated data.
(iv) The answer to the fourth question posed at the beginning, whether a correction of the unconditional ML estimates leads to a better approximation of the Z values to the chi-square distribution, does not appear by Fig. 2.
Theoretically, a decrease of Z values - and thus a better adjustment - is to be expected since the values of the likelihood functions are decreased more greatly by such a correction in the denominator of λ than in the numerator. This tendency was actually evident in the simulated data but the extent of the changes was so slight that the attempt to optimize the test statistic in this manner was not pursued any further.
In short, the simulation studies showed that the LR test can be recommended without reservation for large numbers of items (k > 30). When choosing an extreme significance level the test also makes reliable decisions possible for smaller numbers of items (k < 15).
Conclusion
It has been argued that the availability of different goodness of fit tests related to different assumptions of the model is necessary, since it is not possible to test the fit of the Rasch model as such, that is, with all its assumptions. But even the statistical test of a single assumption of the model is only possible in relation to a certain alternative hypothesis set up by the test constructor. Thus, Andersen's likelihood ratio does not test person homogeneity as such, but only tests whether the formed groups of persons, that is, raw score groups or externally defined groups, are mutually heterogeneous. The same is true for the LR test presented here for testing item homogeneity and for the analogous conditional approach of Martin-Löf (1973). The test of item homogeneity by either an unconditional or a conditional LR test is as strong or as weak as is the grouping of items. Critical groupings of items in order to perform such a test should be derivable from psychological hypotheses about the item response processes. The reported results of the simulation study show the limits of errors of classification, within which the unconditional tests still leads to a significant likelihood ratio. Nevertheless, the test can be applied automatically, for example, by grouping the items according to their difficulty.
This test is also suited to test analogous hypotheses where the data structures are more complex. Rost (1977) used it to investigate the question of whether the learning gain between two test applications was inter-individually constant or whether there were differential learning effects which could be diagnostically relevant. (The computer program is described in Rost, Mach & Kempf (1978))
Dr Jürgen Rost, The University of Kiel
An Unconditional Likelihood Ratio for Testing Item Homogeneity in the Rasch Model, Dr. Jürgen Rost.
Education Research and Perspectives, 9:1, 1982, 7-17.
Reproduced with permission of The Editors, The Graduate School of Education, The University of Western Australia. (Clive Whitehead, Oct. 29, 2002)
REFERENCES
Andersen, E. B. Asymptotic properties of conditional maximum likelihood CMLE estimators. Journal of the Royal Statistical Society, B, (1970) 32, 283-301.
Andersen, E. B. The asymptotic distribution of conditional likelihood ratio tests. Journal of the American Statistical Association, (1971) 66, 335, 630-3.
Andersen, E. B. A goodness of fit test for the Rasch model. Psychometrika, (1973a) 38, 1, 123-40.
Andersen, E. B. Conditional inference for multiple-choice questionnaires. British Journal of Mathematical and Statistical Psychology, (1973b) 26, 31-44.
Birnbaum, A. Some latent trait models and their use in inferring an examinee's ability, in F. M. Lord & M. R. Novick (eds), Statistical Theories of Mental Test Scores, Reading/Mass.: Addison-Wesley (1968).
Fischer, G. H. Einfuhrung in die Theorie psychologischer Tests. Bern: Huber (1974).
Fischer, G. H. & H. Scheiblechner. Algorithmen and Programme fur das probabilistische Testmodell von Rasch. Psychologische Beitrage, (1970) 12, 23-51.
Gustafsson, J.-E. Testing and obtaining fit of data to the Rasch model. British Journal of Mathematical and Statistical Psychology, (1980) 33, 205-33.
Haberman, S. J. Maximum likelihood estimates in exponential response models. The Annals of Statistics, (1977) 5, 5, 815-41.
Kendall, M. G. & A. Stuart. The advanced theory of statistics, Vol. 11. London: Griffin (1973).
Lazarsfeld, P. F. N. W. & Henry. Latent structure analysis. Boston: Houghton Mifflin (1968).
Martin-Löf, P. Statistiska modeller. Anteckningar fran seminarier lasaret 1969-70 utarbetade av Rolf Sundberg. 2:a uppl. (Statistical models. Notes frona seminars 1969-70 by Rolf Sundberg. 2nd ed.) Stockholm: Institut för försäkringsmatematik och mathematisk Statistik vid Stockholms Universitet (1973).
Neyman, J. & E. L. Scott. Consistent estimates based on partially consistent observations. Econometrica (1948), 16,1.
Rasch, G. Probabilistic models for some intelligence an attainment tests. Copenhagen: Nielsen & Lydiche (1960). (Chicago, University of Chicago Press, 1980.)
Rost, J. Diagnostik des Lernzuwachses. Ein Beitrag zur Theorie and Methodik von Lerntests. Arbeitsbericht 26. Kiel: IPN (1977).
Rost, J., Mach, G. & W. F. Kempf. Logistische Test-modelle. In B. Niehusen, H. Hansen, W. F. Kempf, G. Mach & J. Rost, Manual der IPN-Programmbibliothek, Bd. 2, Arbeitsbericht 24. Kiel: IPN (1978).
Wright, B. D. & G. A. Douglas. Conditional versus unconditional procedures for sample-free item analysis. Educational and Psychological Measurement (1977), 37, 47-60.
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/erp2.htm