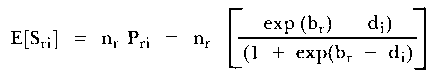
This study compares the use of likelihood ratio chi-square and Pearsonian chi-square fit statistics in the Rasch Model. The analysis, based on simulated data, indicates that the Pearsonian and likelihood ratio chi-square fit statistics correlate .99+ both with data designed to fit the model and under conditions that are designed to simulate measurement disturbances that do not fit the model. A comparison of Type I error rates and the power of the commonly-used Rasch Model fit statistics is also presented.
INTRODUCTION
In several recent journal articles and numerous papers (Hambleton et al., 1978; Gustafsson, 1980; Reckase, 1981) there has been criticism of the fit statistics that are commonly used with the various Rasch Model programs produced by Benjamin Wright and his colleagues at the University of Chicago. Several of these fit statistics are based on the Wright-Panchapakesan (1969) statistic, and are referred to in the literature as the between-group fit statistic. More recently Wright (1980) has developed a weighted [INFIT] and unweighted [OUTFIT] total fit statistic. The introduction of the total fit statistic has led many users to discontinue the use of the between fit statistic particularly when judging the fit of items to the model, although both the total and the between fit statistics can and, perhaps, should be used to test the fit of either items or persons to the model.
The purposes of this paper are threefold:
1. to review some of the sources of this criticism;
2. to relate some findings on the relationship between the Pearsonian chi-square on which the Wright-Panchapakesan fit statistics are based, and the likelihood ratio chi-square; and
3. to examine the Type I error rates and the power of the two commonly-used Rasch fit statistics and the likelihood ratio test.
CRITICISM OF THE FIT STATISTICS
Wright and Panchapakesan (1969) proposed a simple fit statistic for testing the fit of items to the Rasch Model. This test of fit is based on a systematic analysis of the difference between the number of correct responses given by a group of examinees with a similar raw score and the number of correct responses predicted from the model for that group. This predicted value is a function of the difference between a group's estimated ability and an item's estimated difficulty as defined by the following logistic function:
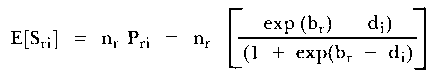 | (1) |
where E[Sri] is the number of right answers to item
i expected in group r,
nr is the number of people in group r
br is the estimated ability of group r
di is the estimated difficulty of item i and
Pri is the probability of a correct response to item i
by any person in group r..
The difference between the observed number of correct responses for a given score group Ori and the expected number of responses on an item forms a residual (Ori - E[Sri]) that represents the degree of departure from expectancy.
Wright and Panchapakesan standardized these residuals by dividing them by the square root of their variance, (P(1 - P)), and then squaring them. This yields an (m x K) matrix of squared standardized residuals, where 'm' is the number of score groups and 'K' is the number of items. They present two fit statistics that are based on this matrix. The first statistic (W-P #1), an overall test of fit for all items, is calculated by summing over all elements in this matrix. When the data fit the model this statistic should be distributed approximately as a chi-square with (m-1)(k-1) degrees of freedom. The second fit statistic (W-P #2) is a test of fit for individual items and is obtained by summing over the m score groups for each item. This statistic is also assumed to have an approximate chi-square distribution with (m-1)(k-1)/(k-(m-1)) degrees of freedom.
Hambleton et al. (1978) stated that the chi-square tests introduced by Wright and Panchapakesan (1969) are of 'dubious validity' if more than a small percentage of the E[Sri] terms in equation 1 have values less than one. They base this statement on the fact that if E[Sri] is less than one the deviates, (O-E) for a particular score group, are not normally distributed and, thus, when squared and summed, will not be distributed as a chi-square. It should be noted that this criticism can be addressed by using reasonable sample sizes and by collapsing across score groups when the E[Sri] for the low ability score groups are less than one.
George (1979) contended that the Z2 statistic is incorrect and that attempts to adjust the simple (Z2/N) formula are 'doomed to failure'. George's first argument was that, since the sample size for any Z2 is always one, the test of fit based on the statistic should be very conservative, i.e., rarely reject items. George suggested that this is due to the fact that the standard deviations of E are large which will make the Z2 values small. He fails, however, to consider the possible values of the residual (O-E) in his consideration of 'large'. If this comparison is made it is clear that the standard deviations are small when compared with unexpected responses, as shown below.
For example, in the dichotomous Rasch model the observed value can be only zero or one. Given this constraint, consider the case where the probability of a person responding correctly is .80. With this probability the residual can take only one of two values, 0.20 for a correct response and -0.80 for an incorrect response. The standard deviation of the residual is the standard deviation of the probability of a correct response which is defined as (P(1-P))1/2, or 0.40 in this example. This value may be large when compared with the standard deviations of residuals based on more observations, as George notes, but it is not large when compared with the possible values that the residual can take in this model, 0.20 and -0.80.
George's second objection is based on the use of a normal approximation to the binomial distribution which he claims is implicit in the expectation that the Z2 is chi-square distributed. Though this specific criticism may be valid in theory, this study and previous studies (Mead and Wright, 1980) have shown that when data are generated to fit the Rasch model the Z2's are approximately normally distributed with a mean of 0 and a standard deviation of 1.
Van den Wollenberg (1979) suggested that the (W-P #1) statistic is not chi-square distributed since its degrees of freedom are incorrect. He felt that the degrees of freedom should be m*k not the (m-1)(k-1) reported by Wright and Panchapakesan. Van den Wollenberg raised a second objection to the assumption that the squared residual in the (W-P #1) statistic is a unit normal deviate. This objection is based on the fact that the observed frequency of any score group is used in the estimation of the item parameter, which is in turn used in the estimation of the E in equation 1.
Van den Wollenberg (1979, 1980) reported that the Andersen likelihood ratio test (1973) and the Wright-Panchapakesan statistic are insensitive to violations of the dimensionality axiom. He proposed two new statistics - Q1, which is very similar to the (W-P #1) statistic, and Q2 , which has no direct counterpart but is based on a pairwise comparison of items. He goes on to suggest that the (W-P #1) statistic can be corrected by including a factor (k-1)/k. This correction is very large for the short tests that he uses in his examples (k = 4), but is very close to 1 in longer tests used in most measurement situations. Corrections based on test length involving the (W-P) statistics are more fully discussed by Smith (1982).
Gustafsson (1980) contended that the tests of fit based on the comparison between observed and theoretical expected frequencies (Wright and Panchapakesan, 1969; Mead, 1976a,b) are inappropriate since the distribution of the test statistics based on the unconditional estimation procedure (JMLE) is unknown. Gustafsson argued that the conditional estimation procedures allow the use of goodness of fit tests which have asymptotically-known distributions (Andersen, 1973). This is true in tests of fit involving items only. In the case of person fit statistics the item difficulties are considered as known parameters and the criticism is not valid.
Gustafsson recommended the use of the Martin-Löf procedure (1973) for testing variations in the person parameters for discrete groups of items. This is a conditional likelihood ratio test which is based on the conditional estimates of the item parameters and does not require the estimation of person abilities. This is an overall test of fit that is applied to samples and cannot be applied to test the fit of an individual person or item.
Reckase (1981) criticized the (W-P #1) statistic stating that, as the probability of a correct response departs from 0.5, the distribution of observed frequencies becomes less and less normal. Thus, the squares of the statistics are less well approximated by chi-squares. He and his colleagues have used the squared difference between the actual responses and expected responses for items, but note that the distributional properties of the fit statistics are unknown and the importance of differences detected is hard to interpret.
Waller (1981) made one suggestion on the use of the (W-P) statistics. He urges that when sample sizes are small (N<1000) the likelihood ratio chi-square test of fit should be used. Waller claimed that this use is suggested by the fact that the Pearsonian chi-square tests of fit do not perform as well as the likelihood ratio chi-square in small sample sizes. This performance will be directly tested in this paper.
THE STUDY
This study will focus on three primary areas of concern. The first is the relationship between the Pearsonian chi-square fit statistic and the likelihood ratio fit statistic suggested by Waller and used by Levine and Rubin (1979) in studies on detecting measurement disturbances. The second is the issue of Type I error rates and power in the current versions of the Rasch and likelihood ratio statistics. Finally, the third is a discussion of which statistics should be used for tests of fit.
There are three person fit statistics that will be used in these studies: the unweighted total fit statistic [OUTFIT], the unweighted between fit statistic, and the likelihood ratio fit statistic. The unweighted between group fit statistic is calculated as follows:
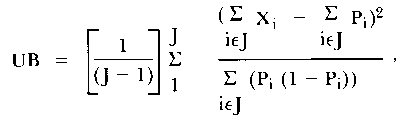 | (2) |
where Xi is the response of the person to item
i,
Pi is the probability of a correct response to item
i, and
J is the number of subsets of items.
This fit statistic is based on the difference between a person's observed score on a subset of items and the score on that subset as predicted by the person's overall ability estimate. The variance of this statistic is believed to be approximately (2/(J-1)). This statistic can be transformed into a statistic that is symmetric about zero by using a [Wilson-Hilferty] cube root transformation (Wright, 1980).
The unweighted total person fit statistic is calculated as follows:
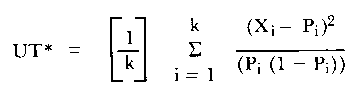 | (3) |
where k is the number of items.
This fit statistic is based on the squared standardized difference between the expected and observed scores for each item on the test. The variance of UT (Wright, 1980) is given as follows:
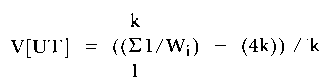 | (4) |
where W = (Pi (1 - Pi)).
* The unweighted total fit statistics reported here were corrected for test length and item dispersion. (See Smith, 1982.)
This statistic can also be transformed into a statistic that is symmetric about zero by using the cube root transformation.
The likelihood ratio fit statistic is defined as follows:
| LR = -2 loge (L0 / L1) | (5) |
where L0 = Π fi (xi;
b0)
and L1 = Π fi (xi; b1
; b2; . . . bJ).
The likelihood ratio test is based on the ratio of the likelihood of the response pattern based on a single overall ability estimate and the likelihood of the response pattern based on the J estimated subset abilities. Here J is the number of subsets of items chosen for the analysis. When the J subsets have the same ability parameter, LR is distributed as a chi-square with (J-1) degrees of freedom. It is the uniformly most powerful test of fit. As a means of comparison with the Rasch statistics, the LR chi-square was transformed into a statistic symmetric about zero using the cube root transformation.
This analysis is based on simulated data. In the first part of the study 1,800 individuals' responses were generated to fit the Rasch Model. The abilities ranged from -1 to +1 logits (-1, -0.5, 0, 0.5, 1) with a uniform distribution. The test used in these simulations was 30 items in length, had an average item difficulty of 0, and a range in difficulty from -2 to +2 logits. The item difficulties were taken from an existing test. They were based on calibration samples that contained 5,000 cases. The item difficulties are considered as known, not estimated, in this analysis.
In the second part of the study responses were generated to simulate two different types of measurement disturbances. To simulate random measurement disturbances ten sets of responses containing 100 replications each were generated utilizing four levels of guessing. One of these sets of responses represented guessing on all 30 items. The other nine sets of responses represented guessing on 1/3, 1/2, and 2/3 of the test items. For each of these levels of guessing, three different levels of ability were used for the non-guessing items: -1, 0, and +1 logits.
In order to generate the simulated responses the probability of a correct response was generated for each non-guessing item/person interaction. This probability was compared with a random number between 0 and 1. If the random number was less than the probability of a correct response, the response was set at 1 and otherwise 0. In the case of the guessing items the random number was compared with 0.25, the probability of guessing a four-choice multiple choice item correctly. If the random number was less than 0.25, the response was set equal to 1 and otherwise 0.
To simulate systematic measurement disturbances nine sets of responses containing 100 replications each were generated. In these simulations one subset of items was made differentially familiar, i.e., the ability used to generate one subset on 10 items was higher than the ability used to generate the remaining 20 responses. This closely represents the condition that would occur if an individual encountered a set of items on a test that were biased in his favor. The differences in generation abilities for the different subsets ranged from 0.5 logits to 3 logits.
The three person fit statistics mentioned above were calculated for each of the simulated cases and the summary of these results is presented below.
RESULTS
To examine the similarity between the transformed likelihood ratio chi-square and the unweighted between fit statistic, the values for both statistics were correlated for the 1,800 cases simulated to fit the model. The correlation between these statistics was 0.9985 in the null case (see Table III for frequency distribution).
| TABLE I CORRELATION BETWEEN LRT AND UB* (Systematic Measurement Disturbance) | |||
|---|---|---|---|
| Generating Ability | Correlation | ||
| Sub 1 | Sub 2 | Sub 3 | |
| 0.0 0.0 0.0 0.0 0.0 -0.5 -0.5 -1.0 -1.5 |
0.0 0.0 0.0 0.0 0.0 -0.5 0.0 0.0 0.0 |
0.5 1.0 1.5 2.0 2.5 2.5 0.5 1.0 1.5 |
.9993 .9993 .9991 .9980 .9965 .9948 .9986 .9987 .9968 |
| * Each line of the table is based on 100 replications. Sub[test] 1 is the first 10 items, Sub 2 the second 10 items, and Sub 3 the last 10 items on the 30 item test. | |||
| TABLE II CORRELATION BETWEEN LRT AND UB* (Random Measurement Disturbances) | ||
|---|---|---|
| No. of Items Guessing |
Ability Non-guess |
Correlation |
| 10 10 10 15 15 15 20 20 20 30 | 1.0 0.0 -1.0 1.0 0.0 -1.0 1.0 0.0 -1.0 - | .9985 .9975 .9955 .9976 .9979 .9953 .9977 .9984 .9950 .9944 |
| * Each line of the table is based on 100 replications. The 'No. of Items Guessing' represents the number of items at the end of the response string with random responses. The non-guessing ability is the ability used to generate the other responses on the 30 item test. | ||
For the 19 cases of simulated measurement disturbances the correlation between the transformed likelihood ratio statistic (LRT) and the unweighted between fit statistic (UB) ranged from 0.9944 to 0.9995. These values are shown in Tables I and II.
It seems clear from these results that the two statistics were measuring the same thing. The close similarity of the results suggests that the two statistics may be asymptotically equivalent to each other.
Using the 1,800 cases that were simulated to fit the model, it was possible to determine the Type I error rates for the three statistics calculated. These values are shown in Table III.
| TABLE III DISTRIBUTION OF FIT STATISTICS | |||
|---|---|---|---|
| Value of Fit Statistic |
Unweighted Total |
Unweighted Between |
Likelihood Ratio T |
| -3.0 to -2.5 -2.5 to -2.0 -2.0 to -1.5 -1.5 to -1.0 -1.0 to -0.5 -0.5 to 0.0 0.0 to 0.5 0.5 to 1.0 1.0 to 1.5 1.5 to 2.0 2.0 to 2.5 2.5 to 3.0 3.0 to 3.5 3.5 plus |
- 4 35 166 316 456 395 213 107 48 16 15 5 24 |
- - 117 182 306 300 332 288 144 86 33 10 2 - |
- - 117 172 316 284 338 283 143 86 45 14 1 1 |
| 1800 | 1800 | 1800 | |
| Mean S.D. n >2.0 % >2.0 |
0.028 0.973 60 3.3 |
0.017 0.974 45 2.5 |
0.039 0.999 60 3.3 |
It would appear that, although the exact distributions of these statistics are not known, the mean, standard deviation and the incidence of Type I error suggest that the use of the normal approximation for obtaining critical values may be reasonable.
Certainly a value greater than 2 occurs less than 5% of the time when the data fit the model. These data lend support to the idea that, for a 30 item test, the use of a critical value less than 2.0 is possible and perhaps more appropriate. Assuming a one-tailed test, the use of this value would approximate the widely-used criterion of 0.05 for Type I error.
Turning to the 19 samples that were generated to simulate some form of measurement disturbance, it is possible to begin to assess the power of these fit statistics to detect such disturbances. Let us first examine the case where one of the subsets (10 items) was differentially more familiar than the remaining items. The ability of the three fit statistics to detect the varying levels of departure from a single overall ability are shown in Table IV.
| TABLE IV DETECTING SYSTEMATIC MEASUREMENT DISTURBANCES* | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Generating Abilities |
Total | Between | LRT | |||||||
| Mean | S.D. | N>2 | Mean | S.D. | N>2 | Mean | S.D. | N>2 | ||
| 0.0 0.0 0.0 0.0 0.0 0.5 |
0.5 1.0 1.5 2.0 2.5 2.5 |
0.23 0.31 0.57 0.90 0.95 1.12 |
0.88 0.71 1.00 1.06 1.03 1.07 |
3 1 5 6 6 9 |
0.27 0.62 1.14 1.69 2.06 2.60 |
0.92 1.10 1.18 1.12 1.04 0.89 |
7 12 22 46 62 79 |
0.27 0.61 1.14 1.71 2.13 2.66 |
0.92 1.09 1.21 1.16 1.11 0.95 |
7 12 22 46 62 79 |
| * Each line of the table is based on 100 replications. The first column represents the generating ability on the 20 item subset and the second column represents the generating ability on the 10 item subset. | ||||||||||
It is clear from these data that the unweighted total is completely ineffective in detecting this type of systematic measurement disturbance. Even when the generating ability of one ten-item subset is 3 logits higher than the generating ability for the other 2 subsets, only 9 of the 100 cases have a total fit statistic greater than 2. The unweighted between and the transformed likelihood ratio perform equally well in this case. However, it is necessary to have a difference of 2 logits or more, about 4 standard errors of measurement in these data, to have a 50-50 chance of detecting the disturbance with either fit statistic. Even for the relatively large difference of 1.5 logits between the two generating values, there is only 1 chance in 4 that the disturbance will be detected. Differences smaller than that are almost impossible to detect with any consistency. [This situation may be detected by principal components analysis of residuals.]
The detection of this type of differential familiarity is even more difficult if there are three sets of items with different generating abilities. This type of situation might occur if there were three sets of items on a test such that one favoured males, one favoured females, and one favoured neither sex. These results are presented in Table V.
| TABLE V DETECTING SYSTEMATIC MEASUREMENT DISTURBANCES* | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Generating Abilities |
Total | Between | LRT | ||||||||
| Mean | S.D. | N>2 | Mean | S.D. | N>2 | Mean | S.D. | N>2 | |||
| -0.5 -1.0 -1.5 |
0 0 0 |
0.5 1.0 1.5 |
0.43 0.63 0.98 |
1.14 0.94 0.75 |
4 5 10 |
0.58 1.49 2.41 |
1.14 1.15 0.83 |
13 39 76 |
0.58 1.49 2.42 |
1.15 1.16 0.86 |
14 39 75 |
| * Each line of the table is based on 100 replications. The first column represents the generating ability for the first 10 item subset. The second column represents the generating ability for the second 10 item subset. The third column represents the generating ability for the third 10 item subset. | |||||||||||
Again, it is obvious that the unweighted total fit statistic is ineffective in detecting this type of systematic bias. Even in the case where there was a 3 logit difference in the generating abilities, only 10 of the 100 cases misfit. By the time there is a 3 logit difference, the unweighted between and the transformed likelihood ratio test are able to detect about 3 out of every 4 cases. Unfortunately, when this difference is as small as 2 logits these two tests are able to detect only 1 in every 3 cases.
In the case of a less systematic type of measurement disturbance, ye.g. random guessing, several interesting things are apparent.
| TABLE VI DETECTING RANDOM MEASUREMENT DISTURBANCES* | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No. of Guess Items |
Total | Between | LRT | |||||||
| Ability | Mean | S.D. | N>2 | Mean | S.D. | N>2 | Mean | S.D. | N>2 | |
| 10 10 10 15 15 15 20 20 20 30 |
1.0 0.0 1.0 1.0 0.0 -1.0 1.0 0.0 -1.0 - |
0.10 0.41 0.79 0.84 0.78 1.11 2.73 2.82 2.77 3.58 |
0.92 0.91 1.55 0.75 1.13 1.53 1.52 1.54 1.97 1.69 |
1 4 16 7 9 26 71 73 65 80 |
1.12 0.46 0.33 1.12 0.66 0.37 2.03 1.13 0.64 0.48 |
1.03 1.01 .95 .99 1.04 1.15 1.11 1.10 1.11 1.19 |
20 3 1 22 11 9 53 26 13 9 |
1.26 0.53 0.36 1.23 0.72 0.36 2.16 1.20 0.64 0.46 |
1.13 1.08 0.97 1.08 1.09 1.14 1.21 1.16 1.14 1.18 |
31 9 2 29 14 9 59 25 13 9 |
| * Each line of the table is based on 100 replications. | ||||||||||
First, in the case of all random responses to the 30 item test, the total fit statistic is able to detect 8 of every 10 cases, i.e., the fit statistic is larger than the chosen value of 2. The between and the likelihood ratio tests are only able to detect about 1 in every 10 cases of guessing. Secondly, neither the LRT nor between fit statistics are very successful at detecting guessing for low ability students, where it is hypothesized that most guessing occurs.
In the case of random responses to ten items, one-third of the test, the total fit statistic was able to detect 16 of 100 cases for the low ability groups while the between and the likelihood ratio could detect less than 2 in 100. Even when two-thirds of the responses were randomly generated, the between and the likelihood ratio tests can detect only between 13 and 53 of every 100 cases. The total fit statistic does considerably better, detecting between 2/3 and 3/4 of the cases.
One of the reasons that the between fit test and the likelihood ratio test fail to do a better job of detecting guessing may be that they are designed for the more specific task of detecting systematic differences in ability. Thus a more general fit statistic, such as the total fit, has an advantage for detecting guessing or other random measurement disturbances.
CONCLUSION
There are several conclusions that can be drawn from the studies presented here.
1. Despite its `problems', the Wright-Panchapakesan between fit statistic can be used instead of the likelihood ratio test of fit.
2. Although there is a lack of knowledge concerning the distribution of the unweighted total and the between tests of fit, it is possible to estimate the power and the Type I error rates for these two statistics. These results suggest that the statistics can be useful in detecting measurement disturbances in a person's responses.
3. Given the Type I error rates reported here, it does not seem unreasonable to use a critical value in the 1.75 to 2.00 range for these statistics, given the acceptance of a one-tailed test.
4. The power studies suggest that if we desire to be able to detect a wide variety of measurement disturbances, it is necessary to use both the total and the between fit statistics. Using only one or the other will miss a variety of disturbances. The use of the likelihood ratio test alone, as some suggest, will greatly weaken the chances of detecting guessing in low ability students.
5. The power studies suggest that those who insist on using critical values of 3 or more with the total and the between fit statistics are operating in an area where the Type I error rate is less than 0.01 and the power of the test is very low even for large disturbances.
Richard M. Smith and Larry V. Hedges
Comparison of Likelihood Ratio χ2 and Pearsonian χ2 Tests of Fit in the Rasch Model, Richard M. Smith and Larry V. Hedges
Education Research and Perspectives, 9:1, 1982, 44-54
Reproduced with permission of The Editors, The Graduate School of Education, The University of Western Australia. (Clive Whitehead, Oct. 29, 2002)
REFERENCES
Andersen, E. B. A goodness of fit test for the Rasch model. Psychometrika, 1973, 38, 123-40.
George, A. Theoretical and practical consequences of the use of standardized residuals as Rasch model fit statistics. A paper presented at the annual meeting of the American Educational Research Association, San Francisco, 1979.
Gustafsson, J-E. Testing and obtaining fit of data to the Rasch model. British journal of Mathematical and Statistical Psychology, 1980, 33, 205-33.
Hambleton, R. K., H. Swaminathan, L. L. Cook, D. D. R. Eignor & J. A. Gifford. Developments in latent trait theory: models, technical issues, and applications. Review of Educational Research, 1978, 48, 467-510.
Levine, M. V. & D. B. Rubin, Measuring the appropriateness of multiple-choice test scores. Journal of Educational Statistics, 1979, 4, 269-90.
Martin-Löf, P. Statistiska modeller. Antechningar from seminarier lasaret 1969-70 utarbetade av Rolf Sundberg. 2: a uppl. Institutet for forsakrings-matematik och matematisk statistik vid Stockholms universitet, 1973.
Mead, R. J. Assessing the fit of data to the Rasch model. Paper presented at the annual meeting of the American Educational Research Association, San Francisco, 1976.
Mead, R. J. Analysis of fit of data to the Rasch model through analysis of residuals. Unpublished Ph.D. dissertation, University of Chicago, 1976b.
Mead, R. J. & B. D. Wright. A study of the robustness of Rasch model estimation and fit statistics. An unpublished report prepared for the National Board of Medical Examiners, 1980.
Reckase, M. D. The validity of latent trait models through the analysis of fit and invariance. A paper presented at the annual meeting of the American Educational Research Association, Los Angeles, 1981.
Smith, R. M. Methods for assessing the fit of persons to the Rasch model. A paper presented at the annual meeting of the National Council on Measurement in Education, New York, 1982.
Waller, M. I. A procedure for comparing logistic latent trait models. Journal of Educational Measurement, 1981, 18, 159-73.
Wollenberg, A. L. van den. The Rasch model and time limit tests. Unpublished Ph.D. dissertation, Nijmegen: Studentenpers, 1979.
Wollenberg, A. L. van den. On the Wright-Panchapakesan goodness of fit test for the Rasch model. Unpublished manuscript, 1980.
Wright, B. D. `Afterword', in Probabilistic models for some intelligence and attainment tests, by G. Rasch. Chicago: University of Chicago Press, 1980.
Wright, B. D. & N. A. Panchapakesan. A procedure for sample free item analysis. Educational and Psychological Measurement, 1969, 29, 23-48.
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Apr. 21 - 22, 2025, Mon.-Tue. | International Objective Measurement Workshop (IOMW) - Boulder, CO, www.iomw.net |
| Jan. 17 - Feb. 21, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Feb. - June, 2025 | On-line course: Introduction to Classical Test and Rasch Measurement Theories (D. Andrich, I. Marais, RUMM2030), University of Western Australia |
| Feb. - June, 2025 | On-line course: Advanced Course in Rasch Measurement Theory (D. Andrich, I. Marais, RUMM2030), University of Western Australia |
| May 16 - June 20, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 20 - July 18, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Facets), www.statistics.com |
| July 21 - 23, 2025, Mon.-Wed. | Pacific Rim Objective Measurement Symposium (PROMS) 2025, www.proms2025.com |
| Oct. 3 - Nov. 7, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/erp4.htm