Disconnected Subsets, Guttman Patterns and Data Connectivity

Rasch methodology implements conjoint measurement. Ideally, all the Rasch parameters (person, items, raters, tasks, rating-scale thresholds, etc.,) are placed in one measurement frame-of-reference so that the estimate of each parameter is located unambiguously relative to the estimate of every other parameter. Sadly, empirical data often fail to support this ideal. The most frequently encountered failures are extreme scores. If a person succeeds on every item on a standard multiple-choice test, then that person obtains the maximum possible score, 100%, and the Rasch estimate corresponding to that score is infinity. In practice, a finite, but outlying, estimate is reported for Rasch measure corresponding to the extreme score (Wright, 1998). Other failures are fortunately rarer.

Disconnected Subsets

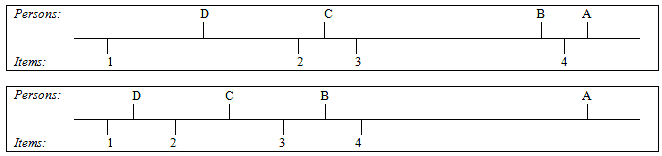
These can be encountered in judge-intermediated data but they sometimes also occur in adaptive or tailored tests and surveys . Table 1 is a simple example of a dichotomous dataset with disconnected subsets.

Persons A and B both scored 1 on Items 1 and 2, so their estimated Rasch ability measures are the same. Persons C and D both scored 1 on Items 3 and 4, so their estimated Rasch ability measures are the same. But how do the estimates for Persons A and B relate to the estimates for Persons C and D? At first glance, they all scored 1 so their estimates are all the same, but this assumes that Items 3 and 4 have the same difficulty as Items 1 and 2. What if Items 3 and 4 were more difficult than Items 1 and 2? Then Persons C and D scored 1 on more difficult items, and so their estimated abilities would be higher than the estimates for Persons A and B. Or, what if Items 3 and 4 were easier? Then Persons C and D would have lower estimates. We see that Persons A and B with Items 1 and 2 are one subset of the data. Persons C and D with Items 3 and 4 are another subset of the data. Estimates of the parameters in one of the subsets cannot be compared unambiguously with estimates of the parameters in the other subset. The disjoint subsets of data are in different frames-of-reference.

Disconnected subsets are not always obvious in rater-intermediated data. The judging plan may specify that each examinee is rated by a pair of raters, and that the pairs of raters change partners according to the judging plan at the start of each judging session. However, unless the raters are carefully supervised, they may not follow the plan. At worst, they may not change partners at all! If this happens, pairs or groups of raters may bring about disconnected subsets of ratings in the data. All the examinees may be rated on the same items, but there are subsets of raters and examinees with no overlap with other subsets of raters and examinees. Accordingly it is vital to start data analysis as soon as the first ratings are collected so that problems in the operation of the judging plan can be quickly identified and remedied before the judging process has been completed.

If disconnected subsets in the data are not identified until after data collection has completed, then constraints must be imposed on the Rasch measures in order to make them approximately comparable. For instance, in a judging situation, we may say that the mean abilities of the examinees in each subset are the same, because the examinees were assigned to judges at random. Alternatively we might say that the mean leniency of the subsets of judges is the same because the judges were assigned initially at random and they had all participated in the same training sessions. However, these constraints inevitable have an arbitrary aspect to them. Some examinees will be advantaged and some disadvantaged. As Shavelson and Webb (1991) remark, it is "the luck of the draw".

Guttman Patterns

Psychometrician Louis Guttman (1916-1987) perceived the ideal test to be one in which a person succeeds on all the items up to a certain difficulty, and then fails on all the items above that difficulty. Then, when persons and items are ordered by raw score, this produces a data set with a "Guttman pattern". A Guttman pattern is shown in Table 2.

These data are very orderly. Person A performed better than Person B, who performed better than Person C, who performed better than person D. But what about measuring the performances? Is the difference between Person A and Person B greater or less than the difference between Person C and Person D? Figure 1 shows two depictions of an additive conjoint latent variable. For both of them, the most likely data is the Guttman pattern in Table 2. There is no information in the data about which of these depiction is more accurate. Georg Rasch perceived that there must be probabilistic disordering ("Guttman reversals") in the data in order to quantify the distance between two elements (persons, items, raters, etc.). A more able person must fail on an easier item, or a less able person must succeed on a more difficulty item in order for the distances between the persons to be additively quantifiable.

Figure 1. Two depictions of a latent variable that accord with the Guttman Pattern in Table 2.

Guttman Splits

Guttman patterns are rarely observed in empirical datasets. The Guttman Coefficient of Reproducibility is rarely 1.0, but there can be unnoticed Guttman Splits in the data. Table 3 illustrates this. In Table 3, every person and item appear to be estimable, because every row and every column has some successes (1) and some failures (0). There are no extreme scores for persons or items. We see that Persons A and B are more able than Persons C and D, also that Items 3 and 4 are more difficult than Items 1 and 2. However, there is a Guttman split between Persons B and C, and between Items 2 and 3. There is no item in the data where Persons A or B fail and Person C or D succeed. Also there is no person in the data for whom there is successs on Items 3 or 4 and failure on items 1 or 2. Persons A, B and Items 3, 4 are all at one location on the latent variable. Also, Persons C, D and Items 1, 2 are all at another location on the latent variable. Regretably, there is no information in the data for estimating the distance between those two locations.

A Practical Example of a Guttman Split

An Olympic Ice-Skating dataset, Exam15.txt in the Winsteps Examples folder, has been analyzed many times. Its estimates are slow to converge, requiring more that 700 iterations through the data, depending on the convergence criteria, much more than the 20 iterations or so required for most datasets. The reason for the slowness in estimation is that there is a Guttman Split in the dataset (which I did not notice for ten years). This is shown in Table 4. Each Judge gave each Skating Performance a score in the range 0.0 to 6.0. These are analyzed as ratings on a scale from 0 to 60. Performance Numbers 1 to 5 all received ratings of 58 and 59. The highest rating given to any of the other 75 Performances is 58. There is a Guttman Split between Performances 5 and 6. We know that the top 5 Performances are better than the other 75 performances, but the data do not tell us how much better in Rasch terms.

Workarounds for Disjoint Datasets and Guttman Splits

The best solution to this type of problem is to analyze the data as they are being collected. Then problems in the data can be identified and remedial action taken before data collection has finished. For instance, the judging plan can be adjusted or extra data can be collected. After data collection has finished, there are two approaches:

(1) Add reasonable dummy data records to the dataset to produce reasonable estimates. The parameters (persons, item, thresholds, etc.) can then be anchored at their reasonable values and the dummy data records omitted for the final reporting. In Table 5, we could add an additional dummy Judge J who gives Performance 5 a rating of 57 and Performance 6 a rating of 58. Now all the Performances can be estimated uniquely in one frame of reference. After anchoring, the dummy Judge would be omitted for the final reporting.

(2) Put reasonable constraints on the estimates. For instance, in Table 4, we might decide that Performance 5 is one logit better than Performance 6. According, Performance 5 is anchored (fixed) at +1.0 logits and Performance 6 at 0.0 logits. The Performances can now be estimated uniquely in one frame of reference. For disconnected subsets, such as Table 1, reasonable constraints may be that the mean ability of the two subsets of persons is the same or the mean difficulty of the two sets of items is the same. Alternatively, the items might be aligned on the latent variable using Virtual Equating (Luppescu, 2005).

John Michael Linacre

Luppescu S. (2005). Virtual Equating. Rasch Measurement Transactions, 19:3 p. 1025. www.rasch.org/rmt/rmt193a.htm
Shavelson, R. J., & Webb, N. M. (1991). Generalizability Theory: A Primer. Thousand Oaks, CA: Sage.
Wright B.D. (1998). Estimating Rasch measures for extreme scores. Rasch Measurement Transactions, 1998, 12:2 p. 632-3. www.rasch.org/rmt/rmt122h.htm

Linacre J.M. (2013) Disconnected Subsets, Guttman Patterns and Data Connectivity. Rasch Measurement Transactions, 27:2 p. 1415-7

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt272b.htm

Website: www.rasch.org/rmt/contents.htm