Majority Rule: the third author

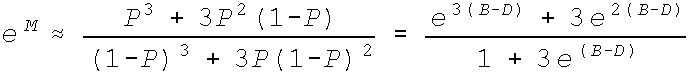
Ben Wright considered three methods of concatenating people (Teams, Packs and Chains, RMT 9:2 432-433). Mallows (1991) proposed another concatenation: majority vote. Wright discovered that adding a low ability person to a Team (required to make unanimous decisions) lowers the success rate of the Team. Mallows discovered that, with majority decisions, even adding a competent person lowers the success rate of a competent group!

If two people of similar abilities Bn and Bm respond to an item of difficulty D independently, but are required to agree on their answer, then the combined Team ability, T, is

T = (Bn - Di) + (Bm-Di) = 2(B-D)
where B is the average of Bn and Bm.

Add a third person of similar ability and permit majority decision making. Then the Majority ability, M, under Rasch model conditions is

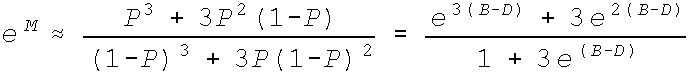
exp(M) = = (exp(3(B-D)) + 3exp(2(B-D)))/(1 + 3exp(B-D))
yielding

1.5(B-D) <= M < 2(B-D)=T when B>=D

which accords with Mallows' pessimism.

In contrast, however, adding a third incompetent person to two other incompetents and allowing a majority vote increases their probability of success!

1.5(B-D) > M > 2(B-D)=T when B<D

Is this why democracy succeeds?

Mallows C (1991) Should you sign up that third author? Chance p. 7.

Majority rule. Wright BD, Mallows C. … Rasch Measurement Transactions, 1995, 9:3 p.443

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt93c.htm

Website: www.rasch.org/rmt/contents.htm