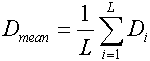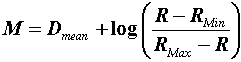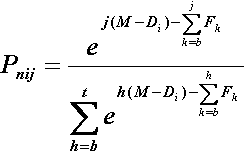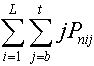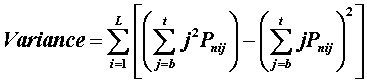Estimating Rasch Measures with Known
Polytomous (or Rating Scale) Item Difficulties
Anchored Maximum Likelihood Estimation (AMLE)
For dichotomies see www.rasch.org/rmt/rmt102t.htm
Once item and step difficulties have been calibrated, we can
administer some or all of the calibrated items to further examinees
and measure them:
1) Collect responses by person n to the desired subset of L
calibrated polytomous or dichotomous items.
Person n has a raw score of R. RMin is the minimum possible score
on these items, RMax the maximum possible.
Make measures (thetas) correspond to extreme scores estimable, instead of infinite, by means of a score correction of 0.3 score-points:
If R = RMin then set R = RMin + 0.3
If R = RMax, then set R = RMax - 0.3
2) Each item i has a calibration Di and each Andrich threshold (step) j a calibration
Fj in user-scaled Rasch units. If not already in logits, convert these to logits.
3) The average item difficulty of person n's L items is
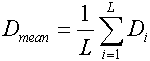
| (1) |
4) The initial estimate of person n's ability M (theta) can be any finite value.
Convenient ones are the mean item difficulty, a previous ability estimate, or
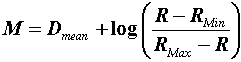
| (2) |
5) Compute expected score and variance for M. The categories for
item i of difficulty D i are numbered b,..,t. Fb=0, and the other Fk are the Rasch-Andrich step thresholds. The denominator
is the sum of the numerators for all categories, so that the sum of the probabilities across all categories is 1:
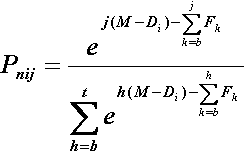
| (3) |
|
Expected Score = | 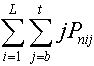
| (4) |
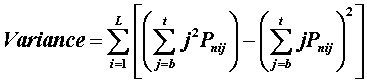
| (5) |
where e = 2.7183, and current estimate of person S.E. = 1/√(Variance).
For "Partial Credit", replace Fk by Fik,
or replace j(M - Di) - ΣFk by jM - ΣDik, and
replace h(M - Di) - ΣFk by hM - ΣDik, with the same
subscript ranges as above.
Dichotomous items are exactly the same as Partial Credit items with only two categories.
Dik=Di. Fik=0.
6) Obtain a better estimate M' of the measure M:
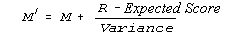
| (6) |
If the estimates overshoot, then multiply the divider by 2 and set its minimum value at 1.0:
Variance divider = max(Variance*2, 1.0)
7) Stop the iterative process when the change per iteration is less than .01 logits, i.e., if |M'-M|<.01, and go to 8.
Set the measure estimate, M, to M', but do not change the estimate by more than one logit per iteration, i.e., M = max(min(M+1,M'),M-1)
Go back to step 5).
8) Set M=M' and report this final ability estimate (theta) with standard
error = 1/sqrt(Variance). Convert measure and standard error to user-scaled units.
"Variance" is the Fisher statistical information in the observations = Test information function
John Michael Linacre
with typesetting assistance from Stacie Hudgens
This estimation is implemented in the Excel Spreadsheet for polytomous estimation.
Estimating Rasch measures with known polytomous item difficulties.Linacre J.M. … Rasch Measurement Transactions, 1998, 12:2 p. 638.
Warm's (Weighted Mean) Likelihood Estimates (WLE)
For an explanation of WLE, see RMT (2009), 23:1, 1188-9
Warm's bias correction is applied to each MLE estimate, M, to produce a Warm's Mean Likelihood Estimate (WLE), MWLE,
which is almost always closer to the mean item difficulty than M.
person n's WLE estimate = MWLE = M + ( J / ( 2 * I2 ) )
where, for polytomous Rasch items,
J =
Σ( (Σ j³Pnij ) - 3(Σ j²Pnij )(Σ jPnij ) + 2(Σ jPnij )³ )
summed over i = 1,L and j = 0,m
I = test information = Variance
Visual Basic Code to do some of the above.
' Step 1) above
' for the responses
Dim itemcount&
itemcount = 50 ' the number of items
ReDim observedrating&(itemcount) ' for your data for one person
' Collect your data here and compute raw scores here
' code missing data as -1 in observedrating&() and exclude from the raw score
Dim ObservedScore&
' ObservedScore& = The raw score
' Step 2) above
' For the items
ReDim itemdifficulty!(itemcount)
itemdifficulty(1) = 1.23 ' your item difficulties in logits
' all the other items
itemdifficulty(itemcount) = 3.45
' for the ratings
Dim bottom&, top&
bottom& = 1 ' the score for your lowest rating-scale category
top& = 5 ' the score of your highest rating-scale category
Redim stepdifficulty!(top&) ' Rasch-Andrich thresholds of your rating scale
stepdifficulty(bottom&) = 0 ' this is always 0.0
stepdifficulty(bottom&+1) = -3 ' from bottom category to 2nd category
stepdifficulty(bottom&+2) = -1 ' your values go here
stepdifficulty(bottom&+3) = 1
stepdifficulty(bottom&+4) = 3 ' step difficulty into top level
' for the person
' Steps 3) and 4) above
Dim ability!
ability = 2.34 ' an initial logit estimate of ability
' Step 5) above
Dim ExpectedScore!, ModelVariance!
ExpectedScore! = 0
ModelVariance! = 0
ReDim expectation!(itemcount), variance!(itemcount)
Dim item&, logit!, cat&, normalizer!, currentlogit!
Dim value!, expect!, sumsqu!
For item = 1 To itemcount
if observedrating&(item) > -1 then
logit! = ability - itemdifficulty(item)
' compute the category probabilities
' and rating expectation
normalizer = 0 ' this will force the sum of the probabilities = 1.0
expect = 0
sumsqu = 0
currentlogit = 0
For cat = bottom& to top&
currentlogit = currentlogit + logit - stepdifficulty(cat)
value! = Exp(currentlogit)
normalizer = normalizer + value
expect = expect + cat * value
sumsqu = sumsqu + cat * cat * value
Next cat
' expected rating on the item
expect = expect / normalizer
expectation(item) = expect ' matches observed rating
' model variance on the item
variance(item) = sumsqu / normalizer - expect ^ 2
ExpectedScore! = ExpectedScore! + expectation(item)
ModelVariance! = ModelVariance! + variance(item)
endif
Next item
' Steps 6), 7) go here
' they are an elaboration of ...
' ability = ability + (ObservedScore& - ExpectedScore!)/ModelVariance!
' Loop back to step 5) until the change in ability is too small to matter
' Step 8)
' Final ability estimate is reported
' Standard error of ability estimate = 1 / sqrt(ModelVariance!)
' Next step ....
' This computes fit statistics: see www.rasch.org/rmt/rmt34e.htm
' we now have the expected ratings for the items and their model variances
' the observed ratings are observedrating&()
Dim ability!, outfitmeansquare!, infitmeansquare!
ReDim standardizedresidual!(itemcount), residual!(itemcount)
Dim infitmeansquaredivisor!, , activeitem&
outfitmeansquare = 0
infitmeansquare = 0
infitmeansquaredivisor = 0
activeitem& = 0
For item = 1 To itemcount
if observedrating&(item) > -1 then
activeitem = activeitem + 1
residual(item) = observedrating&(item) - expectation(item)
standardizedresidual!(item) = residual(item) / Sqr(variance(item))
If standardizedresidual(item) > 2 Then
' report unexpectedly high rating
ElseIf standardizedresidual(item) < 2 Then
' report unexpectedly low rating
End If
outfitmeansquare = outfitmeansquare + standardizedresidual(item) ^ 2
infitmeansquare = infitmeansquare + residual(item) ^ 2
infitmeansquaredivisor = infitmeansquaredivisor + variance(item)
endif
Next item
' fit for the person
outfitmeansquare = outfitmeansquare / activeitem
infitmeansquare = infitmeansquare / infitmeansquaredivisor
' if outfitmeansquare or infitmeansquare are > 1.5 there is noticeable noisy misfit.
Estimating Rasch measures with known polytomous (or rating scale) item difficulties: Anchored Maximum Likelihood Estimation (AMLE), Linacre J.M. … 1998, Rasch Measurement Transactions 12:2 p. 638.