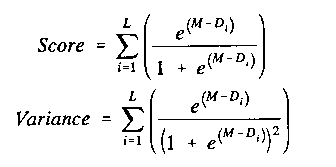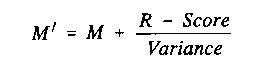1) Collect observed responses by person n to the desired subset of calibrated items.
There are L observed dichotomous responses to L of the calibrated items taken by this person, with R correct answers and W incorrect.
If R = 0, then put R = 0.5, W = L-0.5
If W = 0, then put R = L-0.5, W = 0.5
Check that R+W = L.
2) Each item, i, has a calibration Ui in user-scaled units. If not already in logits, convert this to logits Di.
3) For person n's L observed responses on L items, compute the average item difficulty Dmean and the item sample variance, V:
Dmean = ( Σ Di )/L for i=1,L
V = (Σ (Di - Dmean)² ) / (L-1) for i=1,L
4) An initial estimate of person n's ability M is the PROX estimate:
M = Dmean + (√(1 + V/2.9))*loge(R/W)
alternatively, M = any convenient value
5) Compute expected score and variance for M:
For each item i of difficulty Di, the probability of person n's success on item i = Pi = 1 / ( 1 + e (Di - M) )
where e = 2.7183person n's total raw score = Score = Σ( Pi ) for i=1,L
the model variance of person n's raw score = Variance = Σ( Pi (1 - Pi) ) for i=1,L
6) Obtain a better estimate M' of the measure M:
If, after the first iteration, the estimates overshoot (diverge, so that the changes in the estimates become bigger, not smaller),
abs(M' - M) > abs(M'' - M)
then multiply the divider by 2 and set its minimum value at 1.0:
Variance divider = max(variance*2, 1.0)Do not change an estimate by more than one logit from its value in the previous iteration.
M' = max(min(M+1,M'),M-1)
7) If abs(M' - M) > 0.01 logits, then set M'' = M and M = M' and go to (5).
8) Set M = M', and report this final ability estimate with standard error = sqrt(1/Variance). Convert measure and standard error back to scaled U units for reporting.
Note: Summary statistics for the final person measures may not match directly-estimated person distributional parameters - but, since the persons are often regarded as "incidental" parameters, no one seems too much concerned.